Statistically Improbable Phrases은 Amazon에서 개발한 시스템으로써, 해당 phrase가 얼마나 통계적으로 unique한 것인지를 파악하기 위한 장치입니다. 즉, 한 document에서 uniquely 자주 등장하는 phrase가 있다면,(corpus 전체적으로 봤을 때는 상대적으로 많이 등장하지 않으면서요) 그 phrase를 해당 document의 특징적인 phrase라고 할 수 있겠죠?
한 가지 예로, 만약 의학책이 있다면 해당 책의 SIP(Statistically Improbable Phrases)는 [‘심장수술’, ‘뼈의 구조’, …] 등이 나올 것이고, 법과 관련된 책이 있다면 SIP는 [‘미란다 원칙’, ‘형사소송’, …]등이 나올 것입니다.

아주 똑똑하죠..? 역시 Amazon답네요.. :)
Continue reading
이번에 살펴볼 문제는, 내 컴퓨터에서 파일명에 어떤 원하는 pattern이 포함되어 있는 파일들을 찾아내는 문제입니다. 일단 이 문제를 위해서는 os라는 라이브러리를 사용해야합니다. 그 중에서 listdir이라는 함수는 경로를 인자로 받아서 해당 경로에 있는 파일과 폴더 이름들을 list형태로 리턴해줍니다. 간단한 예를 보시면,
>>> import os
>>> os.listdir('/Users/') #이건 제 컴퓨터의 결과이고, 여러분들은 다 다를 것입니다 :)
['.localized', 'Jacob', 'Shared']
이렇게 쉽게 탐색 결과를 받아올 수 있습니다. 그렇다면, 어떤 것이 폴더이고 어떤 것이 파일인지는 어떻게 알 수 있을까요? 그것은 os.path.isdir이라는 함수를 쓰면 알 수 있습니다.
>>> os.path.isdir('/Users/')
True

이번에 살펴볼 예제는 찢어진 문서의 파편들이 주어졌을 때에 어떻게 original 문서로 복원하는가에 대한 이야기입니다. 각 파편들은 문장 또는 단락의 일부분을 가지고 있는데요, 우리가 조립할 방법은 현재 파편들 중에서 가장 overlap이 많이 되는 두 파편을 골라서 합치고, 또 다시 가장 overlap이 많이 되는 두 파편을 찾고, …, 이런식으로 하나의 문서가 될 때까지 합쳐나가는 방법입니다.
예를들면,
['all is well', 'ell that en', 'hat end', 't ends well']
이런 4개의 파편이 주어졌을 때, 가장 많이 overlap되는 ‘ell that en’과 ‘hat end’를 합쳐서
['all is well', 't ends well', 'ell that end']이 되고,
다시 또 합쳐서 ['all is well', 'ell that ends well']이 되고,
마지막으로 ['all is well that ends well']의 복원된 문서를 갖게 되는 것입니다.
Continue reading
이번엔 네트워크의 중심이 누군지에 관해 찾는 특징 중에 CLOSENESS CENTRALITY에 대해서 알아보겠습니다.
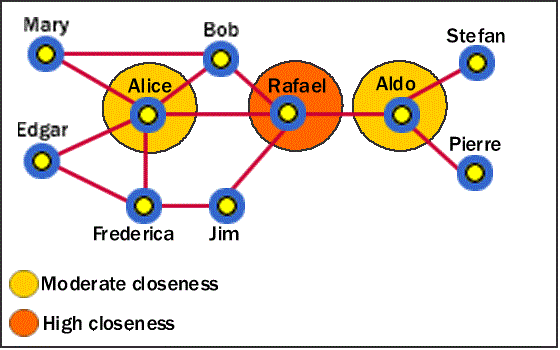
얼마나 많은 connection을 가지고 있느냐로 중심 노드를 결정했던 DEGREE CENTRALITY와 비교해도 꽤나 직관적인 특징입니다.
먼저, 각 노드 $i$는 네트워크의 다른 노드들 $j$에 대해서 shortest path length($d(i,j)$)가 존재합니다. 그리고 이것을 평균 내게 되면 각 노드가 다른 노드에 도달하는데 평균적으로 얼마나 많은 거리를 가야하는지를 알 수 있게 됩니다.
\[El_i=\frac{1}{n-1}\sum_{j\in G, j\ne i} d(i,j)\]
여기서 $El_i$는 $i$노드로부터 다른 노드들까지의 평균 최단거리를 의미합니다. $El_i$가 짧을수록 다른 노드들까지 거리가 짧다는 의미이므로 네트워크의 중심에 자리한다고 볼 수 있을 것입니다.
Continue reading