이번엔 네트워크의 중심이 누군지에 관해 찾는 특징 중에 CLOSENESS CENTRALITY에 대해서 알아보겠습니다.
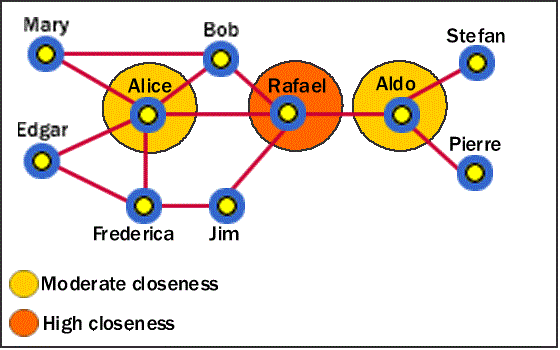
얼마나 많은 connection을 가지고 있느냐로 중심 노드를 결정했던 DEGREE CENTRALITY와 비교해도 꽤나 직관적인 특징입니다.
먼저, 각 노드 $i$는 네트워크의 다른 노드들 $j$에 대해서 shortest path length($d(i,j)$)가 존재합니다. 그리고 이것을 평균 내게 되면 각 노드가 다른 노드에 도달하는데 평균적으로 얼마나 많은 거리를 가야하는지를 알 수 있게 됩니다.
\[El_i=\frac{1}{n-1}\sum_{j\in G, j\ne i} d(i,j)\]
여기서 $El_i$는 $i$노드로부터 다른 노드들까지의 평균 최단거리를 의미합니다. $El_i$가 짧을수록 다른 노드들까지 거리가 짧다는 의미이므로 네트워크의 중심에 자리한다고 볼 수 있을 것입니다.
실제로는 모든 Dijkstra path의 길이를 구해서 평균을 내고 해야겠지만, 어차피 그 컨셉 자체는 심플하기 때문에 그냥 내장되어 있는 함수를 사용하도록 하겠습니다.(예제는 wikipedia 투표 결과입니다.)
>>> import networkx as nx
>>> g = nx.read_edgelist('Wiki-Vote.txt', create_using=nx.DiGraph())
>>> closeness_cent = nx.closeness_centrality(g) #매우 연산적으로 비쌉니다.
>>> sorted(closeness_cent.items(), key=lambda x:x[1], reverse=True)[:10] #상위 10개의 중심 노드를 출력해봅니다.
[(u'766', 0.18720843320883898),
(u'457', 0.1866059095978065),
(u'2565', 0.18600863538076548),
(u'11', 0.18500544110439568),
(u'1166', 0.17593063365065395),
(u'1549', 0.1743427385540616),
(u'2688', 0.17376951906212734),
(u'1151', 0.16936487708905126),
(u'1374', 0.16793022142044142),
(u'1133', 0.16527530539468888)]위에 주석에도 달려있지만, 모든 pair에 대해서 최단거리를 구해야 하므로 연산이 매우 많이 필요합니다. 따라서 오래 걸리겠죠?
그럼 마지막으로 우리가 앞서 구했던 DEGREE CENTRALITY와 비교해보겠습니다.
>>> degree_cent = nx.degree_centrality(g)
>>> sorted(degree_cent.items(), key=lambda x:x[1], reverse=True)[:10]
[(u'2565', 0.16404273263986505),
(u'1549', 0.11695248805172898),
(u'766', 0.10865898228844531),
(u'1166', 0.10444194545965702),
(u'11', 0.10444194545965702),
(u'457', 0.10289569862243464),
(u'2688', 0.08687095867303908),
(u'1374', 0.07745290975541186),
(u'1151', 0.07632836660106831),
(u'5524', 0.0756255271296036)]순위에 차이는 있지만, 거의 결과가 겹치는 것을 확인하실 수 있죠? :) 마찬가지로 Closeness centrality도 좋은 metric이 된다는 것을 알 수 있었네요 :)