이번에 살펴볼 Centrality의 지표 중의 하나는 BETWEENNESS CENTRALITY입니다. 단어 그대로 해당 노드가 얼마나 다른 사람들 관계 사이에서 중요한지를 나타내는 지표가 되겠습니다.
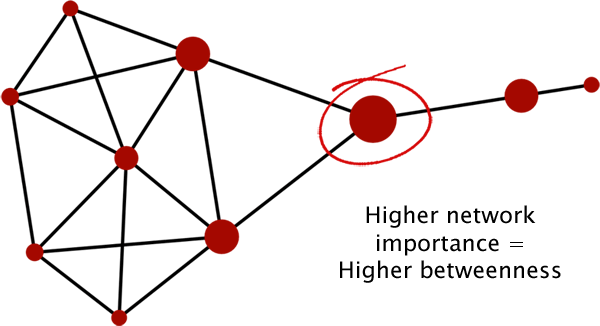
Betweenness를 구하는 방법은 아래와 같습니다.
- 각 노드의 pair마다 Dijkstra shortest path를 계산합니다.
- 각 노드마다 shortest path가 몇 개나 거쳐가는지를 체크합니다.
즉, 해당 노드가 얼마나 서로간의 관계 사이에 존재하는지를 알 수 있겠죠? 만약 중요한 사람이라면 여러 사람의 관계에 모두 사이에서 관계되어 있을 것입니다. 그렇기 때문에 또 하나의 중요한 지표가 될 수 있겠죠? :)
그럼 일단 Bow-tie Network를 만들어서 자세히 살펴보겠습니다.
import networkx as nx
bow = nx.Graph()
bow.add_edge('F', 'G')
bow.add_edge('F', 'E')
bow.add_edge('F', 'D')
bow.add_edge('G', 'D')
bow.add_edge('G', 'E')
bow.add_edge('E', 'D')
bow.add_edge('A', 'D')
bow.add_edge('C', 'D')
bow.add_edge('B', 'D')
bow.add_edge('A', 'B')
bow.add_edge('A', 'C')
bow.add_edge('B', 'C')
%matplotlib inline
nx.draw_networkx(bow)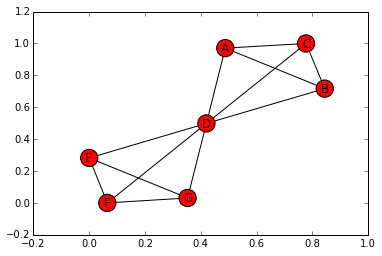
위와 같이 나비넥타이 모양으로 생긴 네트워크를 Bow-tie 네트워크라고 부릅니다. 이 네트워크의 betweenness를 조사해 보겠습니다.
>>> nx.betweenness_centrality(bow)
{'A': 0.0, 'B': 0.0, 'C': 0.0, 'D': 0.6, 'E': 0.0, 'F': 0.0, 'G': 0.0}뭔가 그림에서 직감하셨겠듯이, D가 가장 높고 유일하게 0이 아닌 betweenness를 갖습니다. 그러면 우리가 앞서 살펴봤던 wikipedia 투표 결과를 통해 앞서 살펴봤던 degree, closeness centrality까지 함께 비교해 보겠습니다.
g = nx.read_edgelist('Wiki-Vote.txt', create_using=nx.DiGraph())
deg_cent = nx.degree_centrality(g)
close_cent = nx.closeness_centrality(g)
bet_cent = nx.betweenness_centrality(g)
# Top 10 노드들을 추출합니다.
deg_top10 = sorted(deg_cent.items(), key=lambda x:x[1], reverse=True)[:10]
close_top10 = sorted(close_cent.items(), key=lambda x:x[1], reverse=True)[:10]
bet_top10 = sorted(bet_cent.items(), key=lambda x:x[1], reverse=True)[:10]
names = set([x[0] for x in deg_top10+close_top10+bet_top10])
name = []
degree = []
closeness = []
betweenness = []
for n in names:
name.append(n)
degree.append(deg_cent[n])
closeness.append(close_cent[n])
betweenness.append(bet_cent[n])
#잘 정리된 표로 보기위해서 pandas를 사용합니다.
import pandas as pd
d = {'name':pd.Series(name), 'degree':pd.Series(degree), 'closeness':pd.Series(closeness), 'betweenness':pd.Series(betweenness)}
table = pd.DataFrame(d)표로 정리된 주요 노드들은 다음과 같습니다.
... betweenness closeness degree name
0 0.000000 0.185005 0.104442 11
1 0.005803 0.175931 0.104442 1166
2 0.011563 0.130651 0.057773 15
3 0.000000 0.165275 0.056087 1133
4 0.017654 0.186009 0.164043 2565
5 0.005202 0.150939 0.067613 2328
6 0.000000 0.187208 0.108659 766
7 0.004715 0.153273 0.059320 2237
8 0.000000 0.186606 0.102896 457
9 0.004564 0.134524 0.035845 28
10 0.005438 0.152220 0.061288 5079
11 0.000000 0.173770 0.086871 2688
12 0.002879 0.167930 0.077453 1374
13 0.006135 0.138838 0.065083 737
14 0.003857 0.150999 0.075626 5524
15 0.016564 0.174343 0.116952 1549
16 0.002620 0.169365 0.076328 1151
17 0.008012 0.154499 0.044701 72그렇다면 이 centrality들이 지니는 의미는 어떻게 될까요?
| Metric | Low Degree | Low Closeness | Low Betweenness |
|---|---|---|---|
| High Degree | Ego는 cluster에 포함되어 있긴 하지만, 나머지 네트워크 부분에서 멀리 떨어져 있습니다. | Ego의 connection들은 잉여스럽습니다. 딱히 그것들을 지날 필요가 없는 것입니다. | |
| High Closeness | 몇 안되는 connection이지만 중요한 사람들에 연결되어 있습니다. | Ego는 dense, active cluster의 중심에 다른 많은 사람들과 함께 있습니다. |
네트워크 이론에서 단순히 수치를 구하는 것보다 그 수치들이 지니는 의미를 파악하고 알맞게 해석하는 것이 관건입니다 :)