이번에 살펴볼 예제는 Numpy와 더불어 Scipy를 이용하여 주어진 데이터에 우리가 원하는 함수 꼴로 Model을 fitting하는 예제입니다. 앞서 R을 이용해 linear model을 만드는 것을 알아보기도 했었는데요, python의 scipy library를 이용하여 어떻게 model을 fitting하는지 알아보겠습니다. 먼저 다양한 수학적 tool과 자료구조를 위해 numpy를 import하겠습니다. 그리고 model fitting을 위해 scipy.optimize에서 curve_fit을 import하겠습니다.
>>> import numpy as np
>>> from scipy.optimize import curve_fit이제 linear model을 fitting하기 위해서 데이터 x에 대해서 함수값 y를 리턴해주는 함수를 선언하겠습니다.
## y=ax+b를 리턴합니다.
def func(x, a, b):
return a*x + b본격적으로 fitting되는 것을 확인하기 위해서 먼저 x데이터를 0~10까지의 100개 구간으로 선언하겠습니다.
>>> x = np.linspace(0, 10, 100) #0에서 10까지 100개의 구간으로 나눕니다.
>>> print x
[ 0. 0.1010101 0.2020202 0.3030303 0.4040404
0.50505051 0.60606061 0.70707071 0.80808081 0.90909091
...
]이제 우리가 이론적으로 확인할 함수 $y=x+2$를 발생시키겠습니다.
>>> y = func(x, 1, 2)
>>> print y
[ 2. 2.1010101 2.2020202 2.3030303 2.4040404
2.50505051 2.60606061 2.70707071 2.80808081 2.90909091
...
]잘 발생됐음을 확인할 수 있죠? :) 이제 여기에 약간의 noise를 섞어보겠습니다. np.random.normal을 통해 $0.9\times\mathcal{N}(0,1)$의 난수를 특정 개수만큼 발생시켜서 $y$값에 더해주겠습니다.
>>> np.random.seed(1)
>>> yn = y + 0.9*np.random.normal(size=len(x))
>>> print yn
[ 3.46191083 1.55042933 1.72666562 1.33735854 3.18290727
0.43366568 4.17639119 2.0219845 3.09521599 2.68465757
...
]값들이 요동치는 것을 보실 수 있죠? 그럼 이제 이 데이터를 바탕으로 1차함수를 fitting해 보겠습니다.
>>> popt, pcov = curve_fit(func, x, yn)
>>> print popt #popt는 주어진 func 모델에서 가장 최고의 fit values를 보여줍니다.
[ 1.02977602 1.90564447]
>>> print pcov #pcov의 대각성분들은 각 parameter들의 variances 입니다.
[[ 0.00075267 -0.00376335]
[-0.00376335 0.02521572]]노이즈에도 불구하고 꽤나 정확하게 원래 값인 $a=1, b=2$의 값을 추정해내는 것을 보실 수 있죠? 그리고 pcov의 대각 성분의 값으로 얼마나 정밀하게 측정된 것인지를 판단할 수 있습니다. (parameter들의 variances입니다.)
그럼 이제 그래프를 그려서 결과를 확인해 봅시다.
>>> import matplotlib.pyplot as plt
>>> plt.scatter(x, yn, marker='.')
>>> plt.plot(x, y, linewidth=2)
>>> plt.plot(x, func(x, *popt), color='red', linewidth=2)
>>> plt.legend(['Original', 'Best Fit'], loc=2)
>>> plt.show()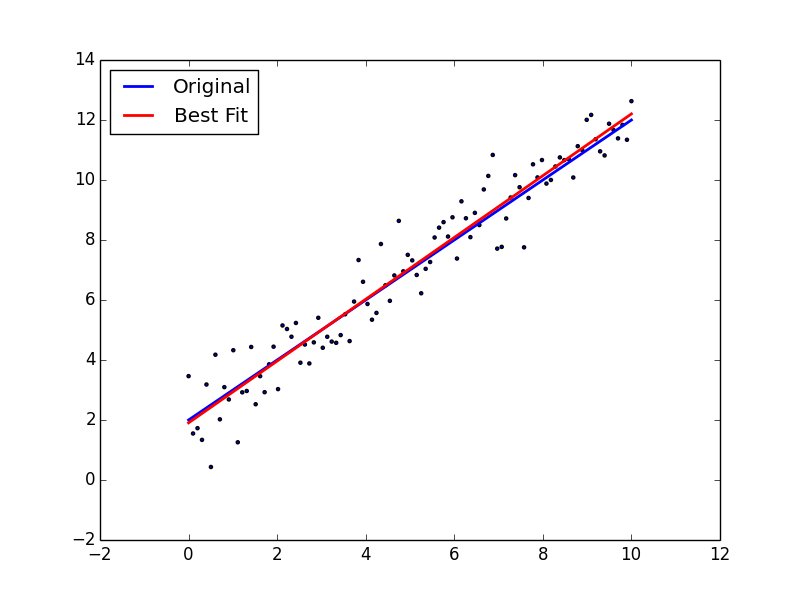
잘 fitting되었음을 확인할 수 있네요 :) 이제 다음으로 선형 모델이 아닌 조금 더 복잡한 Gaussian model을 fitting하는 것을 알아봅시다. \[a\exp\left(\frac{-(x-b)^2}{2c^2}\right)\]
# Gaussian model을 리턴합니다.
def func(x, a, b, c):
return a*np.exp(-(x-b)**2/(2*c**2))
# 마찬가지로 0~10까지 100개 구간으로 나눈 x를 가지고
>>> x = np.linspace(0, 10, 100)
>>> y = func(x, 1, 5, 2) # 답인 y들과
>>> yn = y + 0.2*np.random.normal(size=len(x)) # noise가 낀 y값들을 만듭니다.
## 그런 후에 curve_fit을 하고 best fit model의 결과를 출력합니다.
>>> popt, pcov = curve_fit(func, x, yn)
>>> print popt
[ 1.01217827 5.06673512 -2.09600457]
>>> print pcov
[[ 1.47830098e-03 -4.82758478e-06 2.10848545e-03]
[ -4.82758478e-06 8.41752523e-03 -2.45892661e-05]
[ 2.10848545e-03 -2.45892661e-05 8.80501306e-03]]상당히 정확하게 fitting하죠?? $c$ 값으로 음의 값이 나오는 것은, fitting하는 함수에 $c$가 양수이든 음수이든 상관이 없기 때문입니다.
그럼 이제 그래프로 얼마나 잘 fitting 되었는지 확인해 봅시다.
>>> plt.scatter(x, yn, marker='.')
>>> plt.plot(x, y, linewidth=2, color='blue')
>>> plt.plot(x, func(x, *popt), color='red', linewidth=2)
>>> plt.legend(['Original', 'Best Fit'], loc=2)
>>> plt.show()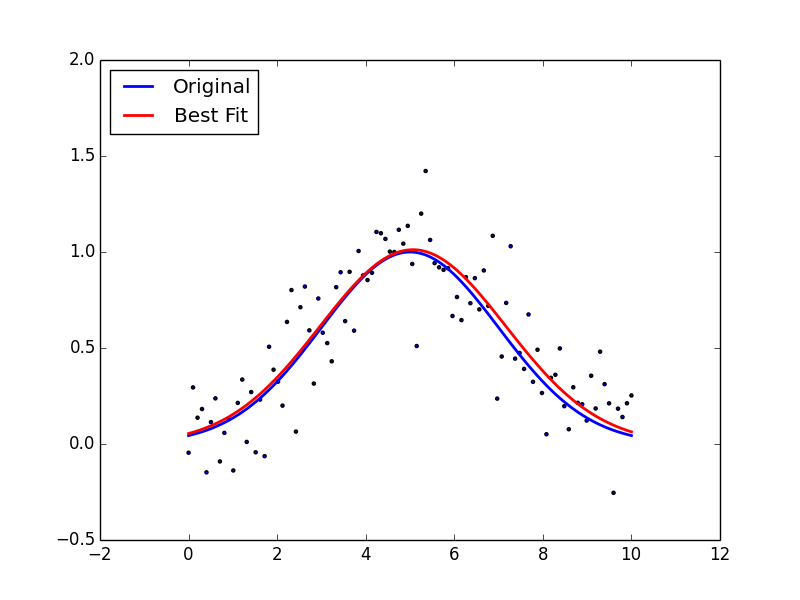
마지막으로 2개의 독립적인 Gaussian함수로 fitting하는 예제를 보여드리겠습니다. \[a_0 \exp\left(\frac{-(x-b_0)^2}{2c_0^2}\right) + a_1 \exp\left(\frac{-(x-b_1)^2}{2c_1^2}\right)\]
def func(x, a0, b0, c0, a1, b1, c1):
return a0*np.exp(-(x-b0)**2/(2*c0**2)) + a1*np.exp(-(x-b1)**2/(2*c1**2))
>>> x = np.linspace(0, 20, 200)
>>> y = func(x, 1, 3, 1, -2, 15, 0.5)
>>> yn = y + 0.2*np.random.normal(size=len(x))
#p0=Initial guess는 초기에 이 값들을 기준으로 optimal value를 찾으라는 설정값입니다.
>>> initial_guess = [1, 3, 1, 1, 15, 1]
>>> popt, pcov = curve_fit(func, x, yn, p0=initial_guess)
>>> plt.scatter(x, yn, marker='.')
>>> plt.plot(x, y, linewidth=2)
>>> plt.plot(x, func(x, *popt), color='red', linewidth=2)
>>> plt.legend(['Original', 'Best Fit'], loc=2)
>>> plt.show()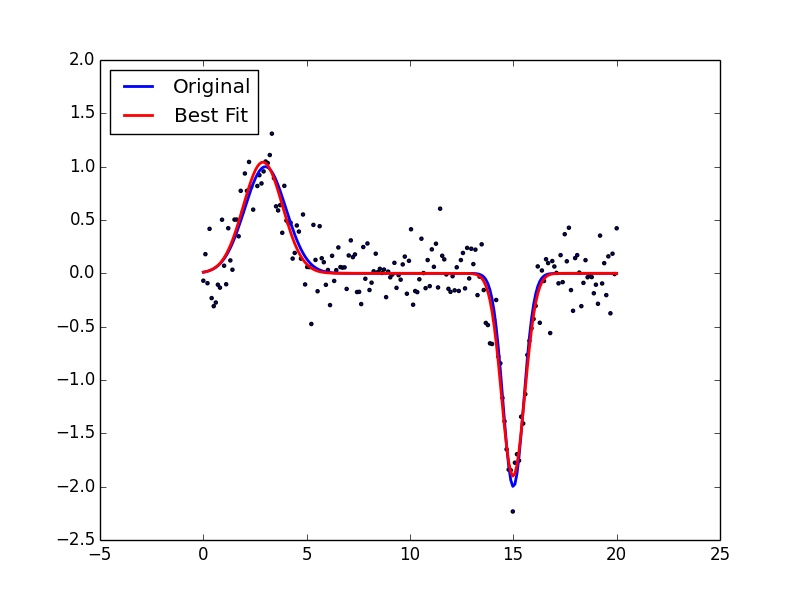
와.. 정말 다양한 함수들을 정의해서 그 최적의 parameters를 찾아주는 방법이 굉장히 심플하죠?? 이렇게 python으로 data analysis부터 plotting까지 완벽하게 소화할 수 있어서 각계각층에서 활용되고 있습니다 :)