이번에 살펴볼 것은 R을 이용한 linear model을 만드는 방법입니다. 이해를 돕기 위해서 MASS library에 포함된 Boston 데이터셋을 사용하겠습니다. 먼저 plot을 이용해 lstat과 medv에 관한 그래프를 그려보겠습니다.
library(MASS)
plot(medv~lstat,Boston)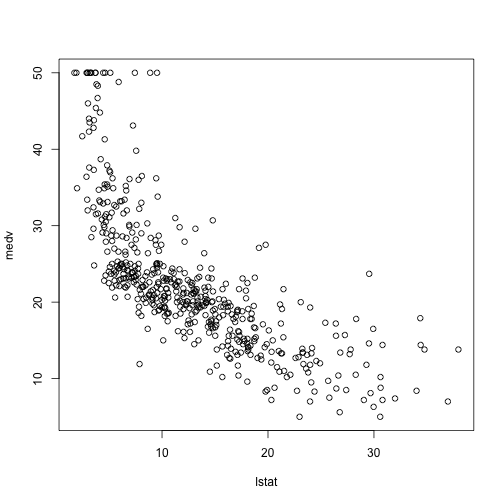
이 데이터에 가장 적합한 직선은 어떤 것일까요? 가장 적합한이라는 것의 정의는 직선에 의해 예측된 값과 실제 값의 차이의 제곱이 최소가 되는 것으로 보통 결정합니다. 즉, 우리가 fit한 linear model이 \[\hat{y}_i=\beta_0 + \beta_1 x_i\]라고 하면, 최소화 해야할 cost function은 \[\sum_{i=1}^n (y_i-\hat{y}_i)^2\]이 되는 것입니다. 여기서 $i$의 의미는 $n$개의 sample들 중 $i$번째 데이터라는 의미입니다. 참고로 $y_i-\hat{y}_i$를 residual이라고 부릅니다.
이렇게 RSS(Residual Sum of Squares)를 최소화하는 방법은 least squares라는 방법으로 쉽게 구할 수 있습니다. 이제 모델을 만들어 보죠.
lm.fit = lm(medv~lstat,data = Boston)
lm.fit##
## Call:
## lm(formula = medv ~ lstat, data = Boston)
##
## Coefficients:
## (Intercept) lstat
## 34.55 -0.95만드는 방법이 굉장히 간단하죠? y~x 형태의 공식을 넣어주시고, 데이터만 명시하면 손쉽게 linear model을 만들 수 있습니다. 그리고 그것을 출력하시면 $\beta_1$과 $\beta_0$를 구할 수 있습니다. 이것을 그래프에 같이 나타내 보겠습니다.
plot(medv~lstat,Boston)
abline(lm.fit, col="red")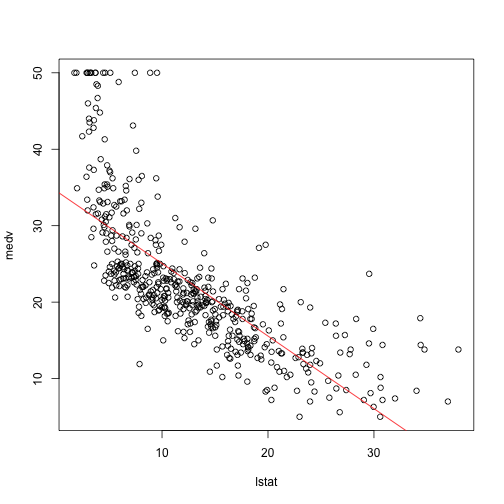
제법 잘 근사된 직선이라는 것을 알 수 있죠? 이것은 사실 엑셀 같은 프로그램의 추세선과 다를 게 없습니다. 가까운 데에 machine learning이 숨어있었네요 :)
그럼 이제 얼마나 잘 만들어진 model인지를 알아볼까요?
summary(lm.fit)##
## Call:
## lm(formula = medv ~ lstat, data = Boston)
##
## Residuals:
## Min 1Q Median 3Q Max
## -15.168 -3.990 -1.318 2.034 24.500
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 34.55384 0.56263 61.41 <2e-16 ***
## lstat -0.95005 0.03873 -24.53 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 6.216 on 504 degrees of freedom
## Multiple R-squared: 0.5441, Adjusted R-squared: 0.5432
## F-statistic: 601.6 on 1 and 504 DF, p-value: < 2.2e-16summary함수를 통해서 각 variable이 실제 response와 얼마나 관련이 있는지를 별표(*)를 통해서 나타내고 있습니다. 별이 세개나 있으니 아주 확실한 선형 관계가 존재한다는 것을 알 수 있겠죠?
그런데 그래프를 보시면 아시겠지만, 아무래도 선형 보다는 2차함수가 더 잘 맞을 것 같죠? ^^ 이제 어떻게 고차방정식을 fitting하는지에 대해 알아보겠습니다.
lm.fit2 = lm(medv~lstat+I(lstat^2),data = Boston)
lm.fit2##
## Call:
## lm(formula = medv ~ lstat + I(lstat^2), data = Boston)
##
## Coefficients:
## (Intercept) lstat I(lstat^2)
## 42.86201 -2.33282 0.04355이렇게 간단하게 고차 방정식들을 fitting할 수 있습니다. 계수들도 확인할 수 있구요.
plot(medv~lstat,Boston)
points(Boston$lstat, fitted(lm.fit2), col='red', pch=20)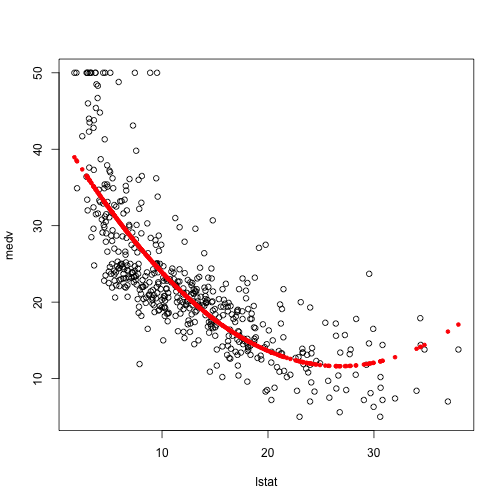
그래프를 보면 훨씬 더 잘 맞는 것 같죠? ^^ 그럼 이제 이 모델이 정확한 것인지 확인해 보겠습니다.
summary(lm.fit2)##
## Call:
## lm(formula = medv ~ lstat + I(lstat^2), data = Boston)
##
## Residuals:
## Min 1Q Median 3Q Max
## -15.2834 -3.8313 -0.5295 2.3095 25.4148
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 42.862007 0.872084 49.15 <2e-16 ***
## lstat -2.332821 0.123803 -18.84 <2e-16 ***
## I(lstat^2) 0.043547 0.003745 11.63 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 5.524 on 503 degrees of freedom
## Multiple R-squared: 0.6407, Adjusted R-squared: 0.6393
## F-statistic: 448.5 on 2 and 503 DF, p-value: < 2.2e-162차 항까지 별표가 세개로 매우 중요하다고 하네요!! 역시 우리의 예측대로입니다. 그럼 이 2차곡선과 직선 중 어느 것이 데이터를 더 잘 표현하고 있을까요? 그것은 바로 R-squared라는 항목으로 비교가 가능합니다. 1에 가까울수록 더 작은 RSS를 갖는다는 의미이죠. 2차 곡선이 0.6407, 직선이 0.5441로써 역시나 예상대로 2차 곡선 모델이 더 정확하게 데이터를 표현하고 있네요 ^^