이번에 살펴볼 알고리즘은 아주 아주 많이 사용되고 또 중요한 Dijkstra 알고리즘에 대해서 알아보겠습니다. 특히나 graph theory에서는 안쓰이는 곳이 없을 정도로 많이 사용되니 반드시 잘 숙지하시면 좋을 것 같네요 :)
Edsger W. Dijkstra라는 computer scientist에 의해 발견된 이 알고리즘은 기본적으로 graph내의 shortest path를 넘어서 weighted graph에서의 minimum cost(weight) path를 찾는 아주 좋은 알고리즘입니다.

원래는 탐색하는 순서에 대한 접근이 달라서 $O(|E|+|V|^2)$의 complexity를 가졌지만, priority queue를 접목시키면서 $O(|E|+|V|\log|V|)$의 complexity로 발전했습니다.(여기서 $|E|$는 Edges의 수를 의미하고, $|V|$는 Vertices의 수를 의미합니다.)
특히나 이 알고리즘은 Artificial Intelligence(인공지능)분야나 Dynamic Programming분야에서 UNIFORM COST SEARCH알고리즘으로 활용되어 아주 무시무시한 활약을 하죠 :) 가장 심플한 예로 아래의 미로찾기를 들 수 있습니다.

우리가 앞서 구현해 놓았던 Priority Queue를 이용해서 구현을 할 것이기 때문에 이것을 저장해 놓은 pq.py라는 파일을 import(작성하시는 파일과 같은 폴더 안에 놓으시고 사용하세요~)해서 그 안에 있는 PriorityQueue클래스를 사용하겠습니다.
from pq import PriorityQueue
def Dijkstra(g, s):
#initialization
dist = {}
prev = {}
Q = PriorityQueue()
#출발노드 s는 자신까지의 거리가 0이고 자신의 predecessor는 없습니다.
dist[s] = 0
prev[s] = None
#다른 노드들은 모두 거리를 +infinity로 설정해주시고 predecessor는 일단 None으로 설정합니다.
#그러면서 PQ에다가 노드들을 넣어줍니다.
for n in g.nodes():
if n != s:
dist[n] = float('Inf')
prev[n] = None
Q.insert(dist[n], n)
#PQ가 빌때까지 계속 루프를 돌면서,
while Q.size() > 0:
p, u = Q.pop() #현재까지 가장 짧은 거리를 갖고 있는 노드를 꺼냅니다.
#꺼낸 노드의 각 이웃들까지의 거리를 현재 자신까지의 minimum cost와 더한 후,
#이웃들이 가지고 있는 거리보다 작으면 이것으로 업데이트 시키고 다시 PQ에 넣거나 update합니다.(우리는 insert기능에 통합시켰었죠 ^^)
for v in g.neighbors(u):
alt = dist[u] + g[u][v].get('weight', 1)
if alt < dist[v]:
dist[v] = alt
prev[v] = u
Q.insert(dist[v], v)
return dist, prev #마지막으로 s부터 각 노드들까지의 거리와 predecessors를 리턴합니다.그럼 이제는 결과를 확인해보기 위해서 우리에게 친숙한 networkx의 krackhardt_kite_graph를 다시한번 이용해 보겠습니다.
import networkx as nx
g = nx.generators.small.krackhardt_kite_graph()
%matplotlib inline
nx.draw_networkx(g, with_label=True, node_color='y')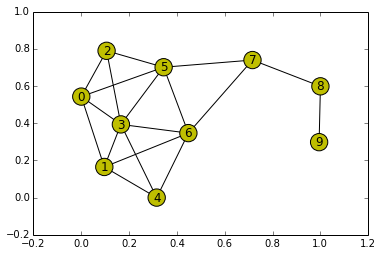
>>> print Dijkstra(g, 0)
({0: 0, 1: 1, 2: 1, 3: 1, 4: 2, 5: 1, 6: 2, 7: 2, 8: 3, 9: 4}, {0: None, 1: 0, 2: 0, 3: 0, 4: 1, 5: 0, 6: 1, 7: 5, 8: 7, 9: 8})
>>> predecessors, distances = nx.algorithms.dijkstra_predecessor_and_distance(g, 0)
>>> print distances, predecessors
{0: 0, 1: 1, 2: 1, 3: 1, 4: 2, 5: 1, 6: 2, 7: 2, 8: 3, 9: 4} {0: [], 1: [0], 2: [0], 3: [0], 4: [1, 3], 5: [0], 6: [1, 3, 5], 7: [5], 8: [7], 9: [8]}networkx의 dijkstra결과와 동일하게 나옴을 확인할 수 있죠? :) 물론 편리하게 구현되어있지만, 우리가 직접 짜봤다는데에 큰 의미를 둘 수 있겠네요 :)
그럼 이 Dijkstra알고리즘으로 구한 Dijkstra path와, 앞서 구한 BFS로 구한 shortest path는 어떤 차이가 있는 걸까요? 그것은 바로 unweighted graph와 weighted graph에서 갈립니다. 현재 g는 unweighted graph이기 때문에 BFS로 구한 shortest path와 Dijkstra path는 동일하게 나올 것입니다.
>>> import itertools
>>> for pair in itertools.combinations(g.nodes()[:5], 2):
... print nx.algorithms.shortest_path(g, *pair), nx.algorithms.dijkstra_path(g, *pair)
[0, 1] [0, 1]
[0, 2] [0, 2]
[0, 3] [0, 3]
[0, 1, 4] [0, 1, 4]
[1, 0, 2] [1, 0, 2]
[1, 3] [1, 3]
[1, 4] [1, 4]
[2, 3] [2, 3]
[2, 3, 4] [2, 3, 4]
[3, 4] [3, 4]완전 동일하게 나오죠?? 그럼 이제 weighted graph를 만들어서 결과를 다시 확인해 보죠.
>>> from random import choice
# 일단 기존의 edges에 random하게 0~9까지의 weight를 부여해서 새로운 weighted edges를 만듭니다.
>>> new_edges = [x + (choice(range(10)),) for x in g.edges()]
>>> print new_edges
[(0, 1, 1), (0, 2, 6), (0, 3, 3), (0, 5, 3), (1, 3, 9), (1, 4, 5), (1, 6, 3), (2, 3, 2), (2, 5, 3), (3, 4, 2), (3, 5, 1), (3, 6, 1), (4, 6, 8), (5, 6, 9), (5, 7, 6), (6, 7, 4), (7, 8, 1), (8, 9, 6)]
>>> g.clear()
>>> g.add_weighted_edges_from(new_edges) #g에 weighted edges를 추가해서 weighted graph로 만들어줍니다.
>>> g[0][1] #weight가 들어가있죠?
{'weight': 1}
>>> for pair in itertools.combinations(g.nodes()[:5], 2):
... print nx.algorithms.shortest_path(g, *pair), nx.algorithms.dijkstra_path(g, *pair)
[0, 1] [0, 1]
[0, 2] [0, 3, 2]
[0, 3] [0, 3]
[0, 1, 4] [0, 3, 4]
[1, 0, 2] [1, 0, 3, 2]
[1, 3] [1, 0, 3]
[1, 4] [1, 4]
[2, 3] [2, 3]
[2, 3, 4] [2, 3, 4]
[3, 4] [3, 4]역시나 path들이 달라짐을 확인할 수 있네요 :)