앞서 BFS(Breadth First Search)에 대해서 알아봤었는데요, BFS의 알고리즘상 가까운 노드부터 검색을 하기 때문에 이론적으로 unweighted(edge들이 모두 동일한 weight를 가지고 있을 경우) graph에서는 BFS를 이용하면 Shortest Path를 찾을 수 있습니다.
그럼 앞서 우리가 예제로 사용했던 간단한 네트워크를 가지고 다뤄보겠습니다.
from networkx.generators.small import krackhardt_kite_graph
import networkx as nx
g = krackhardt_kite_graph() #g는 graph객체가 됩니다.
%matplotlib inline
nx.draw_circular(g, node_color='y', with_labels=True)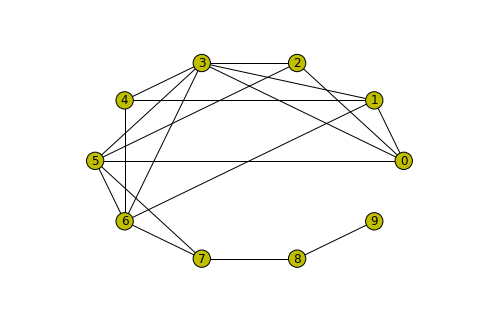
일단 shortest path를 찾는 알고리즘은 BFS와 기본 골자는 같지만, path를 찾아야 하므로 backtrack이 가능한 previous node에 대한 정보를 별도로 기록해야 합니다.
def shortestPathBFS(graph, start, end):
visited = set([start])
prev = {}
queue = [start]
while len(queue)>0:
node = queue.pop(0)
if node == end: #도착 노드를 찾았으면 탐색을 끝냅니다.
break
for neighbor in graph.neighbors(node):
if neighbor not in visited:
queue.append(neighbor)
visited.add(neighbor)
prev[neighbor] = node #queue에 추가하면서 이전노드를 기록합니다.
#python의 특징은 함수 내에 함수가 선언 가능하다는 점입니다!
#도착 노드부터 시작 노드까지 거슬러 올라가면서 path를 만들고 길이와 함께 리턴합니다.
def path(node):
shortest_path = [node]
while node != start:
node = prev[node]
shortest_path.insert(0, node)
return shortest_path, len(shortest_path)-1
return path(node)
>>> shortestPathBFS(g, 0, 9)
([0, 5, 7, 8, 9], 4)그래프 그림을 보면서 살펴보면, 우리의 알고리즘이 잘 동작함을 확인할 수 있네요 :) 일일이 구현해 봤으니 이제 조금 더 편리한 방법을 써 볼까요? 앞서 BFS(Breadth First Search)에서 bfs_tree를 만들어주는 함수가 있다고 했습니다. 이 tree는 directed graph이기 때문에 successor와 predecessor에 대한 정보를 가지고 있고, 이를 이용하면 쉽게 path를 만들어낼 수 있습니다.
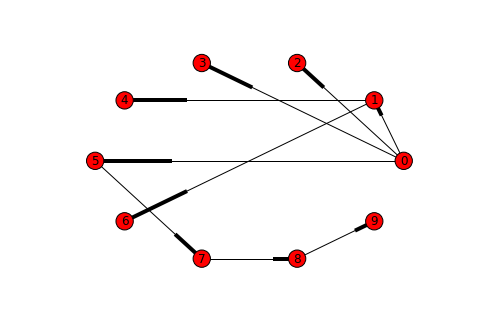
코드로 함께 살펴보죠~
def shortestPathBFS_nx(graph, start, end):
#일단 networkx의 bfs_tree함수로 tree를 만듭니다.
bfs_tree = nx.algorithms.traversal.bfs_tree(graph, start)
#도착 노드부터 predecessor들로 거슬로 올라가면서 path를 완성하고 길이와 함께 리턴합니다.
shortest_path = [end]
while end != start:
end = bfs_tree.predecessors(end)
end = end[0]
shortest_path.insert(0, end)
return shortest_path, len(shortest_path)-1
>>> shortestPathBFS_nx(g, 0, 9)
([0, 5, 7, 8, 9], 4)동일한 결과를 리턴함을 확인할 수 있죠? :) 약간은 더 직관적으로 코딩할 수 있었네요 :) 하지만 역시 라이브러리의 힘은 대단합니다. 이미 우리가 원하는 기능을 몇단계는 더 앞서서 구현해놓고 있네요.
>>> nx.algorithms.shortest_path(g, 0, 9) #networkx의 내장 함수로 한줄로 구할 수 있습니다.
[0, 5, 7, 8, 9]한줄로 구해지다니.. 참 허무하죠? 물론 이것을 처음부터 바로 사용해도 되지만, 일일이 구현해 본 이유는 기본적인 개념과 구현을 한번쯤은 해보는 것이 좋기 때문입니다 :)