아마 네트워크 분석을 하면서 가장 많이 등장하는 스킬(?)이 바로 Depth First Search(DFS)와 Breadth First Search(BFS)일 것입니다. 이들이 가장 기본적으로 graph를 traversing하는 두 가지 방법이기 때문입니다. 가장 자주 등장하면서도 제일 헷갈리고 어려운 개념이기 때문에 잘 습득해 놓아 사용하도록 합시다 :)
Python에서 network analysis를 하기 위해서는 graph를 정의해야 하는데요, 우리가 직접 구현해서 쓸 수도 있겠지만, 아주 powerful하고 편리한 기능을 가진 라이브러리가 있기 때문에 그것을 기반으로 사용하고자 합니다. 바로 networkx라는 라이브러리인데요, numpy, scipy, pandas와 동일하게 아주 요긴하게 사용되는 라이브러리입니다. 그래도 핵심적인 알고리즘이나 컨셉은 가져갈 수 있으니 잘 사용해 봅시다 :)
일단 예제로 사용할 graph로써 networkx에서 제공하는 작은 그래프 하나를 사용하겠습니다.
from networkx.generators.small import krackhardt_kite_graph
import networkx as nx
g = krackhardt_kite_graph() #g는 graph객체가 됩니다.networkx에서는 그래프를 손쉽게 그려주는 좋은 함수들을 가지고 있습니다. 일단 g라는 그래프가 어떻게 생겼는지 그려보겠습니다.
%matplotlib inline
nx.draw_circular(g, node_color='y', with_labels=True)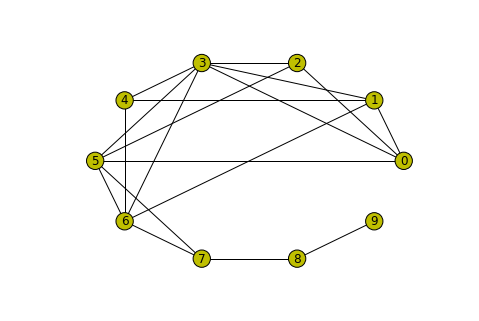
draw_circular라는 이름답게 노드들을 아주 원형으로 이쁘게 배열해 주네요^^ 그러면 이 그래프에 관한 attributes들을 뽑아보는 방법을 알아봅시다.
>>> g.number_of_edges()
18 #총 18개의 모서리가 존재합니다.
>>> g.number_of_nodes()
10 #총 10개의 꼭지점이 존재합니다.(0~9까지)그렇다면 각 노드에 어떤 노드들이 연결되어있는지는 어떻게 알 수 있을까요? Adjacency List는 각 노드가 어떤 노드들에 연결되어있는지 list형태로 가지고 있는 attribute입니다.
>>> g.adjacency_list()
[[1, 2, 3, 5],
[0, 3, 4, 6],
[0, 3, 5],
[0, 1, 2, 4, 5, 6],
[1, 3, 6],
[0, 2, 3, 6, 7],
[1, 3, 4, 5, 7],
[8, 5, 6],
[9, 7],
[8]] #0번 노드가 1, 2, 3, 5번 노드와 연결되어 있습니다...그래프 내의 모든 edge와 node도 쉽게 알아낼 수 있습니다.
>>> g.nodes()
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9] #앞에서 구했듯이 10개의 노드와
>>> g.edges() #18개의 엣지가 있습니다.
[(0, 1),
(0, 2),
(0, 3),
(0, 5),
(1, 3),
(1, 4),
(1, 6),
(2, 3),
(2, 5),
(3, 4),
(3, 5),
(3, 6),
(4, 6),
(5, 6),
(5, 7),
(6, 7),
(7, 8),
(8, 9)]위의 adjacency_list함수를 사용해서 얻을수도 있겠지만, 그래프 내에 neighbors라는 함수를 통해서 해당 노드의 이웃한 노드들을 쉽게 얻을 수 있습니다.
>>> g.neighbors(0) #0번 노드와 이웃한 노드들을 리턴해줍니다.
[1, 2, 3, 5]다른 방법으로 단순히 그래프에 node id로 indexing하면 key에 이웃 노드 id들이 저장된 dictionary가 리턴됩니다.
>>> g[0]
{1: {}, 2: {}, 3: {}, 5: {}}방법은 다양하니 여러분이 편하신 방법을 사용하시면 될 것 같습니다 :) 저는 neighbors함수가 직관적인 것 같아 이것을 주로 씁니다.
그럼 이제 기본적인 툴을 익혔으니, 본격적으로 DFS와 BFS를 다뤄보겠습니다. 먼저 DFS의 알고리즘은 아래와 같습니다.
- 임의의 노드 n을 선택합니다.
- n을 방문했다고 표시합니다.
- n의 방문하지 않은 이웃들에 대해서 다시 DFS를 적용시켜줍니다.

위 그림을 보시니 왜 Depth First인지 아시겠죠? 그럼 코드로 나타내보겠습니다.
def DFS_Nodes(graph, node, visited=[]):
visited.append(node)
for neighbor in graph.neighbors(node):
if neighbor not in visited:
DFS_Nodes(graph, neighbor, visited)
return visited
>>> DFS_Nodes(g, 0) #DFS가 실행되면서 방문한 노드 순서대로 저장된 list를 출력합니다.
[0, 1, 3, 2, 5, 6, 4, 7, 8, 9]networkx라이브러리에서도 dfs_tree라는 함수를 제공하면서 손쉽게 해당 그래프를 주어진 노드로 시작했을 때 얻어지는 DFS tree를 리턴하게 됩니다.
dfs_tree = nx.algorithms.traversal.dfs_tree(g, 0) #0번 노드부터 시작합니다.
nx.draw_circular(dfs_tree, node_color='y', with_labels=True)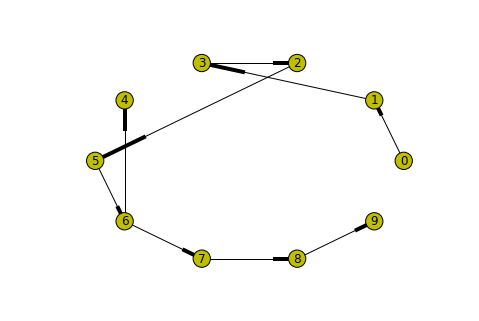
원본 그래프와는 많이 다르죠? DFS특성상 최대한 chain을 만들면서 가게 됩니다. 그리고 원래는 방향성이 없는 undirected graph에서, DFS tree는 방향성을 갖게 되고 이를 directed graph라고 합니다. (그래서 DFS tree는 topological sort에도 사용되게 됩니다.)
>>> type(g), type(dfs_tree) #g는 방향성이 없는 undirected graph이고, dfs tree는 방향성이 있는 directed graph입니다.
(networkx.classes.graph.Graph, networkx.classes.digraph.DiGraph)반면, BFS알고리즘은 아래와 같습니다.
- 노드 n부터 시작하고, 방문했다고 표시하면서 큐에 넣습니다.
- 큐가 empty일때까지 계속 반복하면서,
- 큐에서 첫번째 원소를 뽑습니다. 그리고 뽑은 원소의 방문하지 않은 이웃들을 방문했다고 표시 후에 큐의 끝에 집어넣습니다.

위의 그림을 보시면 DFS와의 차이를 분명하게 아실 수 있을 것입니다. 그럼 코드로 짜보면,
def BFS_Node(graph, node, visited=[]):
queue = [node]
visited.append(node)
while len(queue) > 0:
dequeued = queue.pop(0)
for neighbor in graph.neighbors(dequeued):
if neighbor not in visited:
visited.append(neighbor)
queue.append(neighbor)
return visited
>>> BFS_Node(g, 0) #방문하는 순서가 다르죠?
[0, 1, 2, 3, 5, 4, 6, 7, 8, 9]DFS tree와 마찬가지로 BFS tree도 제공되는 함수로 쉽게 뽑아낼 수 있습니다.
bfs_tree = nx.algorithms.traversal.bfs_tree(g, 0) #0번 노드부터 시작합니다.
nx.draw_circular(bfs_tree, node_color='y', with_labels=True)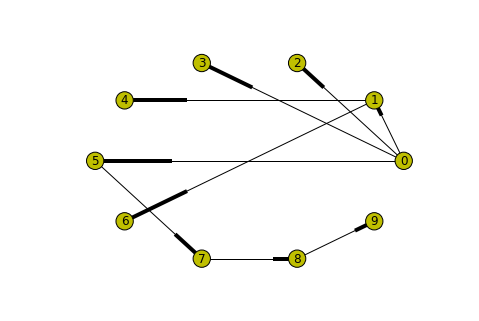
확연히 DFS가 chain형태의 tree를 만들던 것과는 비교가 되죠? 최대한 같은 레벨에서 많은 자식노드들을 가지려고 노력합니다.
쓰다보니 굉장히 길어졌네요. 그래도 그림과 함께, 예제와 함께 알아봤으니 도움이 많이 되셨길 바랍니다 :)