Jacob's Coding Playground

이번에 살펴볼 예제는 Divide and Conquer라는 알고리즘에 있어서 가장 기본적이면서 핵심적인 스킬을 연습해 볼 수 있는 예제입니다. 앞서 Merge Sort와 Quick Sort에서 이미 다뤘던 개념이고, 하나의 큰 문제를 작은 하위 문제들로 나눠가면서 complexity를 크게 줄이는 방법입니다. 먼저 아래와 같은 주식 가격 정보가 있다고 가정해 봅시다. 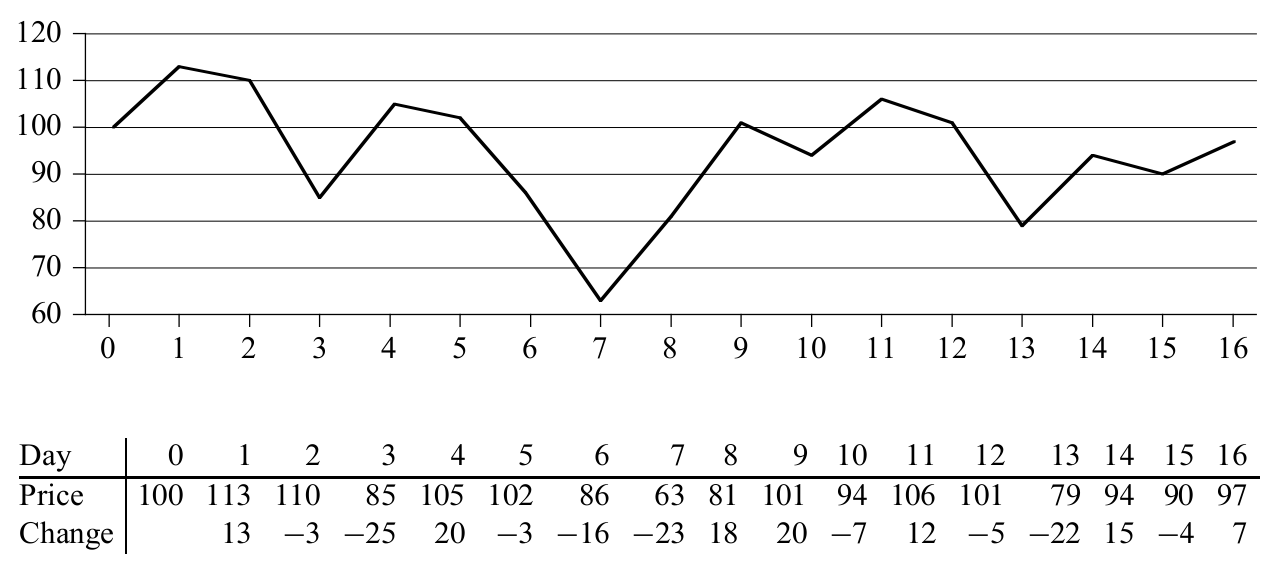딱 한 번 사고 팔 기회가 있다고 가정했을 때, 언제 사서 언제 팔아야 최대의 수익을 낼 수 있을까요?(단, 사는 날짜는 반드시 파는 날짜보다 이전이어야 합니다.)

[문제 출처 : Codechef] K개의 핵 반응로가 있습니다.(0에서 K-1까지의 index를 갖습니다.)

입자들은 0번 반응로로 쏘아집니다.

그렇게 0번 반응로는 N개의 입자까지 모으다가 N+1번째 입자가 쏘아짐과 동시에 1번 반응로로 입자를 이동시키고 자신이 가지고 있던 입자들을 다 파괴시켜버립니다.

마찬가지로 1~K-2번 반응로도 각각 N개까지 모으다가 N+1번째 입자가 들어옴과 동시에 자신+1번째 반응로로 입자를 하나 전달하고 자신이 가지고 있던 모든 입자를 파괴합니다.

K-1번째(마지막) 반응로는 전달할 반응로가 없기 때문에 그냥 N+1번째 입자가 들어오면 모두 파괴시킵니다.

A개의 입자를 쏠 때, K개의 반응로와 각 반응로가 N개의 입자까지 수용할 수 있다고 가정했을 때, 최종적인 반응로들의 입자 분포는 어떻게 될까요?

이번에 도전해 볼 예제는 K-means clustering을 활용한 Image Segmentation입니다. 이미지는 pixel이라는 단위로 구성되어 있는데요, 이 한 pixel당 Red, Green, Blue의 세가지 색상이 각 8bits(0~255)의 값을 가져서 24bits True Color를 완성하게 됩니다. 물론 gray scale로 되어 있는 흑백 사진의 경우 단순히 8bits(0~255)의 값만으로 pixel이 구성되게 됩니다. 그렇다면 그림은 (r, g, b)의 3차원 값을 지닌 dataset이라고 볼 수 있습니다. 만약 이 색깔들을 $K$개의 cluster로 뽑아낸다면, 비슷한 색깔을 지닌 pixel들을 묶어낼 수 있겠죠? 그것 뿐만이 아니라 segmentation을 통해 pixel당 24bits대신에 1~$K$의 index만으로 정보를 축소하여 보낼 수 있겠죠? 그럼 가장 먼저 R에서 아래의 이미지를 불러와 보겠습니다.

K-means clustering은 가장 대표적인 Unsupervised learning 방법 중의 하나입니다. Unsupervised learning이란 response $y$가 없는 상황에서 $x$들의 분포를 가지고 clustering을 하여 정답은 없지만 그래도 가장 합리적인 결과를 얻어내는 것을 의미합니다. 또한 K-means clustering은 우리가 사용할 수 있는 또 다른 feature로서도 활약할 수 있기 때문에 매우 중요하고 효과적인 알고리즘이라고 할 수 있습니다.

[문제 출처 : Codechef] 이번에 살펴볼 문제는 꽤나 복잡한 문제입니다. 얼핏 보기에는 쉬워보이지만 막상 복잡한 구조로 되어있으니 정신 바짝 차라시길 ^.~ 어떤 수 n이 주어졌습니다. 이 n을 $2^x$꼴들로만 구성되게 표현하는 것이 이번 문제입니다. 간단하게 예를 들면, \[15=1111_{(2)}=2^{2+2^0}+2^{2}+2^{2^0}+2^0\] 이와 같이 지수에 있는 숫자들조차도 계속해서 $2^x$꼴로 표현해 나가는 것입니다. 생각보다 헷갈리죠?