K-means clustering은 가장 대표적인 Unsupervised learning 방법 중의 하나입니다. Unsupervised learning이란 response $y$가 없는 상황에서 $x$들의 분포를 가지고 clustering을 하여 정답은 없지만 그래도 가장 합리적인 결과를 얻어내는 것을 의미합니다. 또한 K-means clustering은 우리가 사용할 수 있는 또 다른 feature로서도 활약할 수 있기 때문에 매우 중요하고 효과적인 알고리즘이라고 할 수 있습니다.
K-means clustering은 아래와 같은 방식으로 동작합니다.
- 임의로 각 sample에 cluster를 할당합니다.
- 아래의 과정을 sample에 할당된 cluster가 수렴할 때까지 반복합니다.
(a) 각 $K$ cluster에 속한 점들을 평균 내어서 centroid를 구합니다.
(b) 각 sample들을 가장 가까운 centroid로 분류해 줍니다. (보통 Euclidean distance로 정의된 경우가 많습니다.)
이렇게 반복 작업을 하면서 \[\text{minimize}_{C_1,…,C_K}\left(\sum_{k=1}^K\frac{1}{|C_k|} \sum_{i,i’\in C_k}\sum_{j=1}^p (x_{ij}-x_{i’j})^2 \right)\] Cost function을 최소화하게 됩니다.
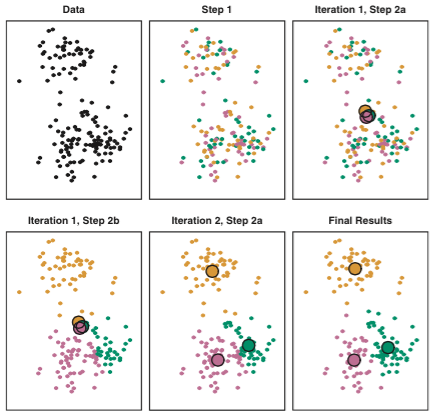
K-means는 어떤 dimension에서도 동작하지만, 우리는 동작하는 것을 보길 원하기 때문에, 일단은 2차원 문제를 생각해 보겠습니다. 랜덤 함수를 통해서 예제 데이터를 생성해 보겠습니다.
set.seed(101) #여러분들도 하실 때 같은 데이터를 얻기 위해서 seed를 지정합니다.
x=matrix(rnorm(100*2),100,2) # 100x2 행렬을 N(0,1) 난수들로 채웁니다.
xmean=matrix(rnorm(8,sd=4),4,2) # 4x2 행렬을 N(0,4) 난수들로 채웁니다.
which=sample(1:4,100,replace=TRUE) # 각 행이 가지게 될 평균을 index로 지정합니다.
x=x+xmean[which,] # 처음 발생시켰던 난수 행렬에 위에서 정해진 평균들을 더합니다.
plot(x,col=which,pch=19) # data를 plot해 봅니다.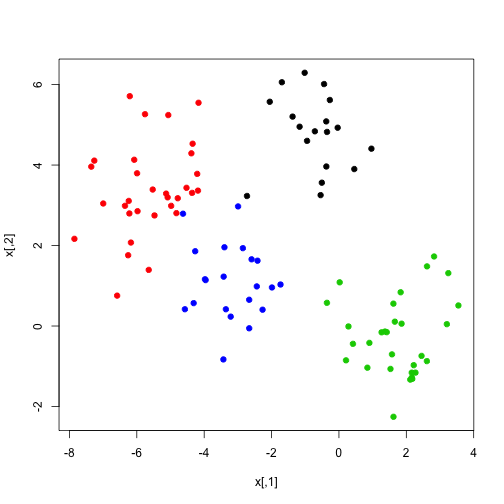
4개의 cluster들이 잘 분포함을 확인하실 수 있죠? 하지만 이 색깔들은 우리만 알고 있는 것입니다. 이제 얼마나 잘 k-means가 분류해 낼 수 있는지 봅시다.
km.out=kmeans(x,4,nstart=15)nstart라는 매개변수는 총 15번을 시행하고 그 중의 minimum 값을 취하라는 의미입니다. 왜 이렇게 여러번을 시행해야 하냐면, 앞서 언급했다시피 우리는 초기에 랜덤하게 sample들에게 초기 cluster를 배정합니다. 이 과정에서 다른 결과들이 나올 수가 있기 때문에 여러 번 해서 최대한 모든 가능한 결과를 찾아보려고 하는 것입니다.
km.out## K-means clustering with 4 clusters of sizes 21, 30, 32, 17
##
## Cluster means:
## [,1] [,2]
## 1 -3.1068542 1.1213302
## 2 1.7226318 -0.2584919
## 3 -5.5818142 3.3684991
## 4 -0.6148368 4.8861032
##
## Clustering vector:
## [1] 2 3 3 4 1 1 4 3 2 3 2 1 1 3 1 1 2 3 3 2 2 3 1 3 1 1 2 2 3 1 1 4 3 1 3
## [36] 3 1 2 2 3 2 2 3 3 1 3 1 3 4 2 1 2 2 4 3 3 2 2 3 2 1 2 3 4 2 4 3 4 4 2
## [71] 2 4 3 2 3 4 4 2 2 1 2 4 4 3 3 2 3 3 1 2 3 2 4 4 4 2 3 3 1 1
##
## Within cluster sum of squares by cluster:
## [1] 30.82790 54.48008 71.98228 21.04952
## (between_SS / total_SS = 87.6 %)
##
## Available components:
##
## [1] "cluster" "centers" "totss" "withinss"
## [5] "tot.withinss" "betweenss" "size" "iter"
## [9] "ifault"K-means의 결과를 살펴보는 것은 매우 쉽습니다. 간략하게 centroid의 값과, 각 sample들이 어떤 cluster에 분류되었는지 등 다양한 정보를 한눈에 요약하고 있습니다 :) 그럼 이제 마지막으로 분류된 결과를 원본 데이터 위에 그려서 비교해 보겠습니다.
plot(x,col=km.out$cluster,cex=2,pch=1,lwd=2)
points(x,col=which,pch=19)
points(x,col=c(4,3,2,1)[which],pch=19)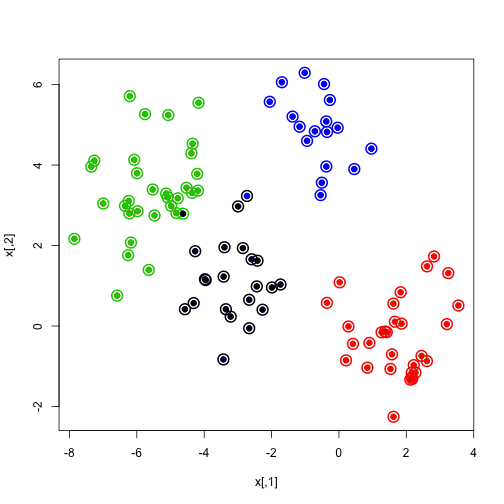
매우 정확한 결과를 가져오죠? 물론 이는 원본 데이터 자체가 잘 분리된 편이기 때문입니다. 정말로 아예 섞여 있는 데이터라면 사실 clustering자체가 동작하기 어려운 여건이겠죠? 또 하나 중요한 것은 실제로 우리는 data에서 K값을 알지 못한다는 것입니다. 따라서 다양한 K를 해 보고 가장 적합한 결과를 갖는 K를 선택하는 것이 매우 중요할 것입니다.