학창시절에 적분이라는 것을 배우면서, 그것을 구하는 방법에 대해 배웠었습니다. 가장 처음 접하는 예가 Riemann integral이라는 방식인데요, 미소구간 $dx$를 잡고 $dx$와 $f(x_i+dx)$를 변의 길이로 갖는 사각형들로 함수 면적을 쪼개서 그 합으로 적분 값을 근사해 나가는 방식입니다. 특히나 이 방법은 analytic한 solution이 없을 경우에 numerical solution을 구하기에 매우 핵심적인 방법입니다. 원리는 간단하지만 얼마나 대단한 방법인지 한번 살펴보시죠 :)
먼저 함수 $f(x)=3x^2+2x-2$라는 함수를 가정해 보겠습니다. 이것은 analytic한 솔루션이 존재하는데, 적분해 보면 \[\int f(x) dx = x^3+x^2-2x+C\] 라는 것을 쉽게 알 수 있습니다. 따라서 만약 우리가 $[0, 10]$구간 내의 적분 값이 궁금하면, \[\int_0^{10}f(x)dx = 1000+100-20=1080\] 이라는 것을 알 수 있습니다. 그럼 이제 이 적분 값을 numerically 구해보도록 하겠습니다. 먼저 $dx=1$로 놓고 (그러면 0~1, 1~2, …, 9~10 이런식으로 10개의 사각형이 생기겠죠?) 끝 구간(1, 2, …, 10)에서의 함수 값을 구해 사각형의 넓이를 구한 후 더함으로써 적분 값을 구해보겠습니다.
dx=1
x=seq(dx,10, by=dx)
y=3*x^2+2*x-2 #함수 값을 구하고,
barplot(y, names.arg=x)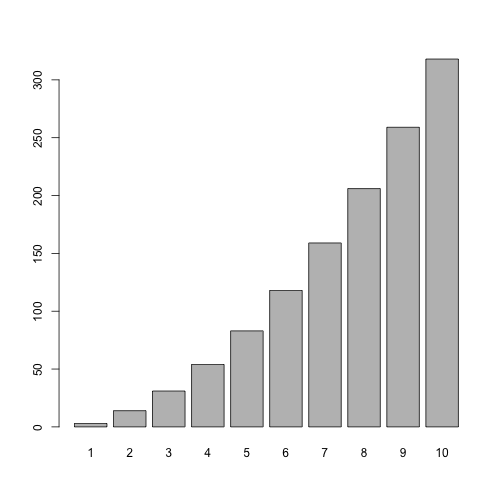
sum(y)*dx #사각형의 넓이의 합을 구합니다.## [1] 1245우리가 구한 정답과 차이가 많이 나네요. 방법이 잘못된 것일까요?ㅠ 하지만 엂핏 위의 그래프를 봐도 꽤나 많은 차이가 있을 것 같네요. 그럼 $dx$를 조금씩 더 좁혀가도록 하겠습니다.
dx=0.1
x=seq(dx,10,by=dx)
y=3*x^2+2*x-2
barplot(y, names.arg=x)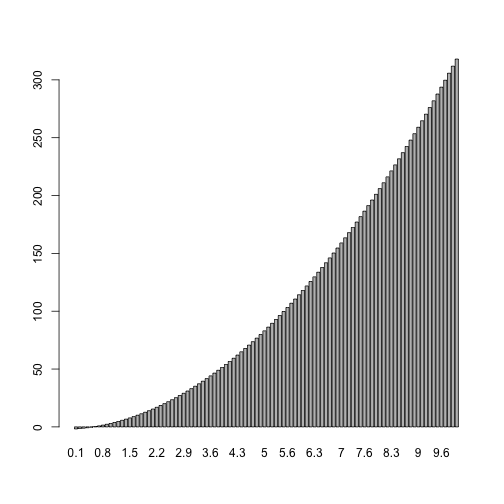
sum(y)*dx## [1] 1096.05dx=0.01
x=seq(dx,10,by=dx)
y=3*x^2+2*x-2
barplot(y, names.arg=x)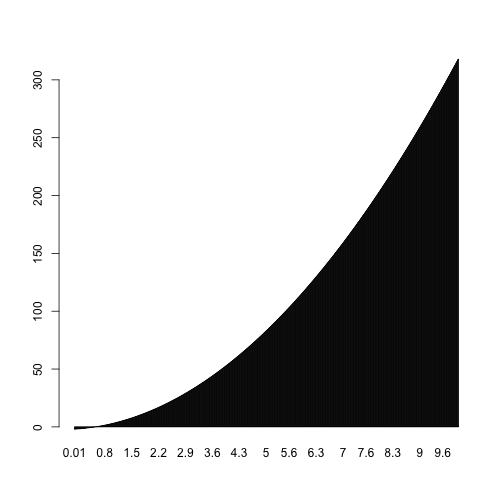
sum(y)*dx## [1] 1081.601dx=0.001
x=seq(dx,10,by=dx)
y=3*x^2+2*x-2
barplot(y, names.arg=x)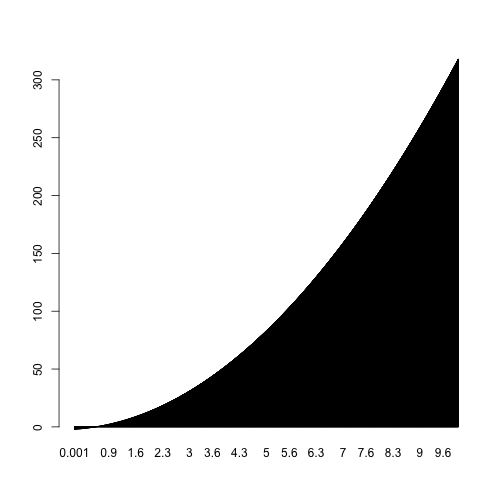
sum(y)*dx## [1] 1080.16그래프로도 확연히 드러나겠지만 점점 더 우리가 알고 있는 참 값으로 근사해 감을 확인할 수 있죠? 이런식으로 $dx\rightarrow 0$일 때, Riemann Sum은 Integral값으로 수렴해 감을 알 수 있습니다 :)