이번에 살펴볼 분야는 제가 학부때에 많이 공부했던 신호처리 분야입니다 :) 그때 당시에는 C언어나 matlab을 사용했었는데, 이렇게 R로 새롭게 해보니까 또 새롭네요. 여기서는 특정 신호를 fft를 이용하여 분석해보고 어떻게 필터를 적용할 수 있는지 살펴보겠습니다.
가장 먼저, 신호를 만들어 볼 텐데요, 주파수가 10인 신호와 25인 sine 함수를 섞은 형태를 가정하겠습니다.
nSample = 101
t = seq(0, 1, length.out = nSample)
f1 = 10
f2 = 25
signal = sin(2*pi*f1*t) + sin(2*pi*f2*t)
plot(t,signal, type='b', pch=20, ylab="Original Signal")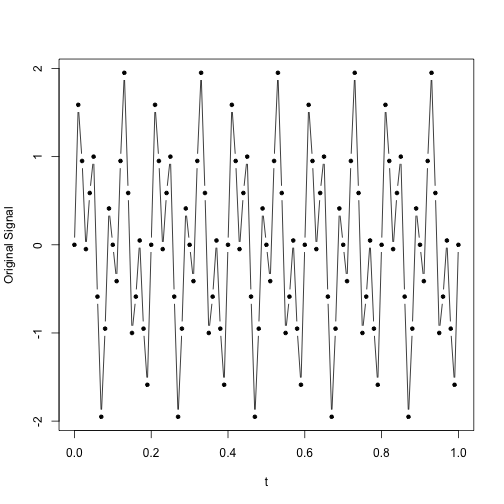
뭔가 주기성은 있는데 신호가 굉장히 안 이쁘죠? 이렇게 시간 축으로 살펴봤을 때는 분석하기 어려운 신호도, Fourier Transform을 이용하면 주파수 축에서 projection 시켰을 때 훨씬 간단해진답니다.
fft_signal = fft(signal)
magnitude = abs(fft_signal)/nSample
magnitude = c(magnitude[(nSample%/%2+1):nSample],magnitude[1:(nSample/2)])
f = seq(-50, 50, length.out = nSample)
plot(f, magnitude, type='b', pch=20, col='blue', ylab="Magnitude")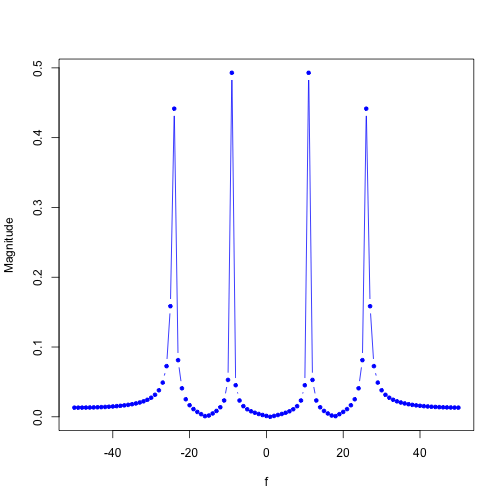
여기서 abs함수를 사용하는 이유는 fft를 하게 되면 그 값이 복소수의 형태로 나오기 때문입니다. 그래서 우리는 세기에 관심을 갖게 되는 것이죠. 물론 phase라고 해서 실수와 허수의 비율을 각도로 계산한 것도 중요한 물리적 성질이 됩니다만, 일단 여기서는 신호의 세기만 가지고 보겠습니다.
또하나 중요한 성질은, fft를 하게 되면 우리가 생각하는 주파수 축이 아니라 양의 축이 먼저 나오고 음의 축이 나오는 형태가 되기 때문에 반드시 shift를 시켜주고 plot을 그려야 옳은 그림입니다.
또한 Nyquist Theorem에 의해서 주파수 축은 $-\frac{f_s}{2}$에서 $+\frac{f_s}{2}$까지의 구간을 갖습니다.($f_s$는 sampling frequency로써, 시간 축에서 몇 초에 한번 data를 취했냐를 의미합니다. 위의 예의 경우 0.01초에 한번 샘플링 했으므로 $f_s=100$입니다.)
세기 그래프를 관찰해 보시면, 정확히 대칭적으로, 그리고 우리가 심어주었던(?) 두 주파수의 신호가 선명하게 나타나는 것을 확인할 수 있죠? 시간 축에서 봤을 때는 굉장히 복잡해 보였는데 말이죠.
그럼 마지막으로 10Hz의 신호만 통과시키는 Low Pass Filter를 적용하여 우리가 원하는 신호만 뽑아내겠습니다.
fft_signal[15:(101-15)]=0
z = fft(fft_signal, inverse = T)/nSample회로적으로는 복잡할 수도 있겠지만, 우리는 시뮬레이션을 하기 때문에.. 필터 적용 자체가 굉장히 간단합니다. 바로 주파수 축에서 14Hz 이상(0부터 시작하기 때문에)을 모두 0으로 만들어 버리는 것이죠. (물론 -14Hz까지는 또 살려줘야 합니다.)
par(mfrow=c(2,1))
plot(t, signal, type='b', pch=20, ylab="Original Signal")
plot(t, z, type='b', col='red', pch=20, ylab="Filtered with Low Pass Filter")## Warning in xy.coords(x, y, xlabel, ylabel, log): imaginary parts discarded
## in coercion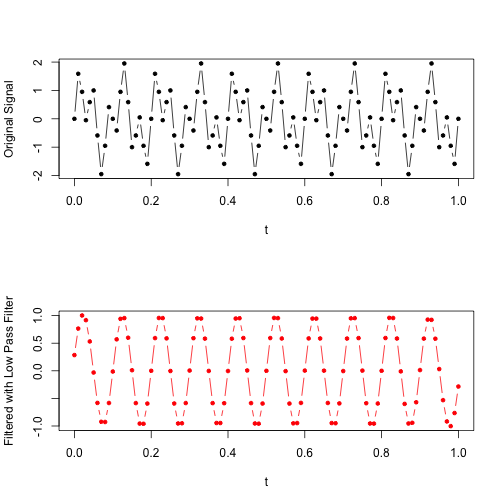
이제 결과 그래프를 확인해 봅시다. 위의 그래프가 원래 우리가 만들었던 10Hz + 25Hz짜리 신호이구요, 아래쪽이 필터된 10Hz짜리 신호입니다. 굉장히 아름답게 추출되어 있는 것을 확인할 수 있죠?
이런 신호처리 기법들을 기반으로 해서 디지털 통신이나 mp3, 이퀄라이저 등의 많은 응용분야가 발생하게 됩니다. 재미있겠죠? :)