이번에 살펴볼 개념은 앞서 Validation Set Approach에서 살펴봤듯이, machine learning에서 필수적인 validation의 한 방법입니다. Validation set approach 방식은 간단하고 빠르게 동작할 수 있지만, 가장 큰 단점으로 매번 다른 random set을 뽑을 때마다 그 결과가 달라질 수 있다는 점을 들었습니다. 이번에 살펴볼 Leave-One-Out CV(LOOCV) 방식은 총 $N$(샘플 수 만큼)번의 model을 만들고, 각 모델을 만들 때에 하나의 샘플만 제외하면서 그 제외한 샘플로 test set performance를 계산하여 N개의 performance에 대해서 평균을 내는 방법입니다.
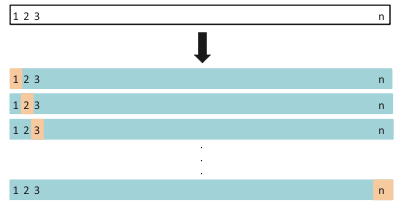
각 sample을 test set으로 삼았을 경우 MSE(Mean Squared Error)를 $\text{MSE}_i$라고 할 때, \[\text{MSE}_i=(y_2-\hat{y}_2)^2\] 가 되고, 우리가 구하려는 성능은 결국 \[\text{CV}_{(n)}=\frac{1}{n}\sum_{i=1}^n\text{MSE}_i\] 이 됩니다.
LOOCV의 장점으로는 결국 모든 샘플에 대해서 다 한번씩은 test하기 때문에 어떠한 randomness도 존재하지 않게 되는 것과, validation set approach와는 다르게 굉장히 stable한 결과를 얻을 수 있다는 점입니다. 또한 하나의 샘플만을 test set으로 사용하기 때문에 그만큼 많은 수의 training data를 활용하여 model을 만들어 볼 수 있게 됩니다. 반면 단점은 그만큼 많은 수의 model을 만들고 test 해야하기 때문에 computing time이 굉장히 오래 걸릴 수 있습니다. 또한 나중에 언급할 k-fold CV에 비해서 model의 다양성을 포함하기 어렵다는 단점이 있습니다.
한편, Least Squares(linear regression 또는 polynomial regression)의 경우에는 computing time을 획기적으로 단축시켜주는 마법의 공식이 있습니다.
\[\text{CV}_{(n)}=\frac{1}{n}\sum_{i=1}^n\left(\frac{y_i-\hat{y}_i}{1-h_i}\right)^2\]
여기서 $h_i$는 leverage입니다. 그러면 이제 실제 데이터를 가지고 LOOCV를 시행해 보도록 하겠습니다. 이번에 사용할 데이터는 ISLR library에 존재하는 Auto 데이터입니다.
library(ISLR)
glm.fit=glm(mpg~horsepower, data=Auto) #mpg를 horsepower에 대해서 linear regression을 힙니다.glm으로 만든 model에 CV를 적용해주는 cv.glm이라는 함수가 있습니다. 이 함수는 boot라는 라이브러리에 있습니다.
library(boot) #cv.glm을 사용하기 위한 라이브러리입니다.
cv.err=cv.glm(Auto, glm.fit) #cv.glm함수를 통해 LOOCV를 시행합니다.
cv.err$delta #delta는 cross-validation 결과들을 담고 있습니다.## [1] 24.23151 24.23114LOOCV의 결과 약 24.23정도의 test MSE를 갖네요. 그럼 이제 위에서 언급한 마법의 공식을 함수로 만들어서 결과가 같게 나오는지 확인해 봅시다.
#linear model, polynomial model에 한해서 LOOCV에 간단한 형태의 공식을 사용할 수 있습니다.
loocv=function(fit){
h=lm.influence(fit)$h
mean((residuals(fit)/(1-h))^2)
}
loocv(glm.fit)## [1] 24.23151앞서 구한 값과 비교해 봤을 때, 똑같음을 알 수 있습니다. 하지만 직접 돌려보시면 알겠지만 정말 속도 차이가 많이 나는 것을 느끼실 겁니다.
그럼 이제 마지막으로 mpg를 horsepower로 설명하고 싶을때, 몇차함수를 fitting해야 가장 미래의 test set에 대해서 잘 예측할 수 있는지 LOOCV를 통해 알아보겠습니다.
cv.error=rep(0,5)
degree=1:5 #1차부터 5차함수까지 fitting해 봅시다.
for(d in degree){
glm.fit=glm(mpg~poly(horsepower,d), data=Auto) #poly함수를 이용해 d차 함수를 fit할 수 있습니다.
cv.error[d]=loocv(glm.fit) #LOOCV 결과를 각 벡터에 저장합니다.
}
plot(degree,cv.error,type="b") #LOOCV 결과를 plot합니다.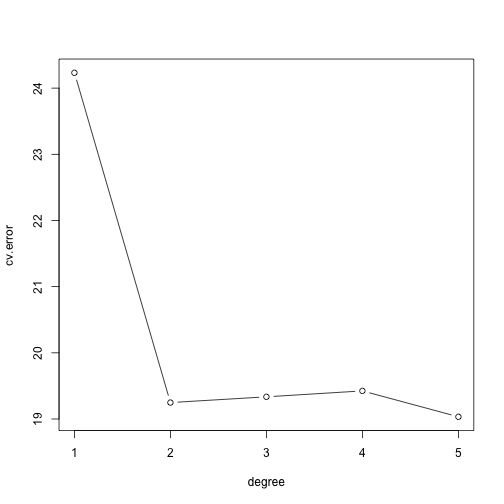
그래프를 보면 5차함수가 가장 낮은 LOOCV error를 가짐을 알 수 있습니다. 반면 2~4차함수 중에서는 2차함수가 가장 잘 fit된 것임을 확인할 수 있죠? 이런식으로 machine learning에서는 CV를 굉장히 많이 사용하고 중요하게 생각합니다. Model의 performance를 평가함에 있어서 굉장히 중요한 척도가 되니까 잘 익혀두시면 좋을 것 같네요^^