이번에 알아볼 예제는 통계에서 없어서는 안될, 아주 많이 쓰이는 R이라는 통계 프로그램을 바탕으로 machine learning의 기본 개념중의 하나인 Maximal Margin Classifier에 대해서 가볍게 살펴보겠습니다.
Learning에는 크게 supervised learning과 unsupervised learning으로 나눌 수가 있는데, Supervised learning은 response, 즉 y값을 가지고 있는 경우이고, unsupervised learning은 response가 없는 상황에서 예측이 아닌 패턴 분석 등을 위해 사용되는 방법을 말합니다.
우리가 이번에 살펴볼 MMC(Maximal Margin Classifier)는 supervised learning 중에서도 classification(y의 값이 연속된 값이 아닌 categorical한 값일 경우)에 사용되는 방법입니다. 먼저 다음과 같은 데이터를 살펴보시죠.
X1 = c(3,2,4,1,2,4,4)
X2 = c(4,2,4,4,1,3,1)
Y = c(rep("Red", 4), rep("Blue", 3))
plot(X1, X2, col=Y, pch=19)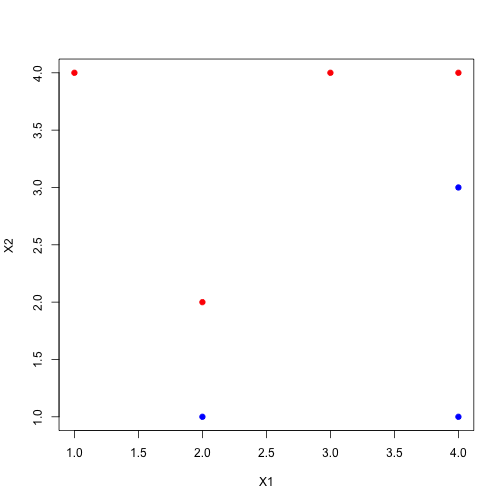
이 빨강 점들과 파랑 점들을 직선을 그어서 나눌 수 있을까요? 이렇게 직선을 통해 나뉠 수 있는 data를 linearly separable data라고 합니다. 어떻게 보면 이상적인 case이죠. 그런데 문제는 이런 linearly separable data에서는 나눌 수 있는 직선이 무수히 많다는 점입니다. 예를 들면,
plot(X1, X2, col=Y, pch=19)
abline(a=-.5, b=1, col=1)
abline(a=0.3, b=0.7, col=1, lty=2)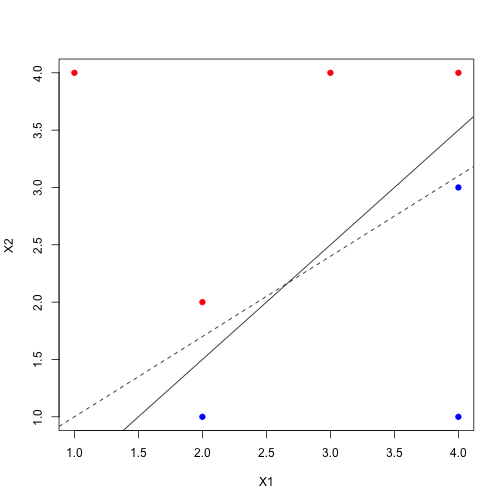
이렇게 여러개의 직선이 데이터들을 완벽히 구분지을 수 있겠죠? 그런데 자세히 보시면 아시겠지만, 점선의 경우 (4, 3)에 걸려있는 점이 조금만 위로 가도 잘못 분류가 되겠죠? 반면 실선의 경우 점들이 조금 요동을 쳐도 꽤나 안정적인 decision boundary가 될 것 같습니다. 이런식으로 decision boundary와 가장 인접한 점들간의 수직 거리를 margin이라고 정의하고, MMC는 이 margin이 최대가 되는 직선을 찾아서 data를 classify하는 것입니다.
여기서의 maximal margin decision boundary(hyperplane 이라고도 합니다.)는 $X_1, X_2 = (2, 1.5)$ and $(4, 3.5)$인 점들을 지나는 직선이고, 이것을 함수로 표현하면, \[-0.5+X_1-X_2=0\]이 됩니다. 그리고 각 $X_1, X_2$의 데이터를 받았을 때에 \[\begin{aligned} -0.5+X_1-X_2>0 &\quad \text{“BLUE”}\newline -0.5+X_1-X_2<0 &\quad \text{“RED”} \end{aligned}\] 이런 식으로 분류를 하면 이것이 classifier가 되는 것입니다.
이제 margin을 찾아봅시다. 그래프를 다시 그려서 hyperplane과 margin을 표시하면 아래와 같습니다.
plot(X1, X2, col=Y, pch=19)
abline(a=-.5, b=1, col=1)
abline(a=-1, b=1, col=1, lty=2)
abline(a=0, b=1, col=1, lty=2)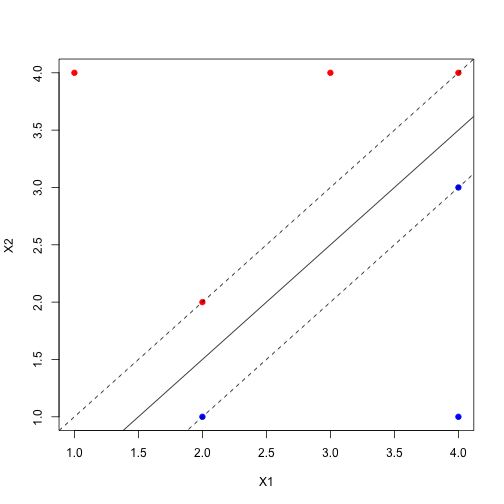
중학교 수학시간에 ‘수직인 직선끼리의 기울기 곱은 -1이다’를 이용하여 수직인 직선의 방정식을 구한 후, hyperplane과의 intersection을 구해 수직거리인 maximum margin을 구하면 0.3535534임을 알 수 있습니다.
그리고 이 때 maximum margin에 정확히 닿아 있는 점들을 support vector라고 표현합니다. 실제로 hyperplane이 이 support vectors에 의해 결정됨을 직관적으로 알 수 있겠죠? (보라색 동그라미 쳐진 점들이 support vector들입니다.)
plot(X1, X2, col=Y, pch=20)
abline(a=-.5, b=1, col=1)
abline(a=-1, b=1, col=1, lty=2)
abline(a=0, b=1, col=1, lty=2)
points(c(2,2,4,4),c(1,2,3,4), cex=2, col='purple')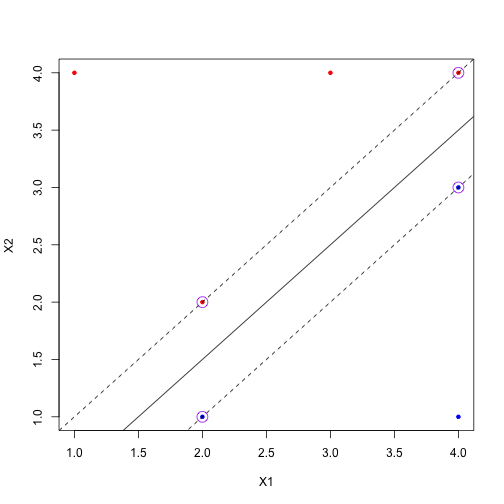
재밌는 점은, support vector가 아닌 점들은 decision boundary를 결정하는 데에 아무 영향도 주지 않는다는 점입니다. 그림을 보시면 당연한 얘기겠죠?
하지만 아쉽게도 만약 data가 linearly separable 하지 않을 경우에는 제약이 따르게 됩니다. 만약 (3.5, 1.5)에 빨간 점을 하나 더 찍는다고 하면,
plot(X1, X2, col=Y, pch=20)
abline(a=-.5, b=1, col=1)
points(3.5, 1.5, col='red', pch=20)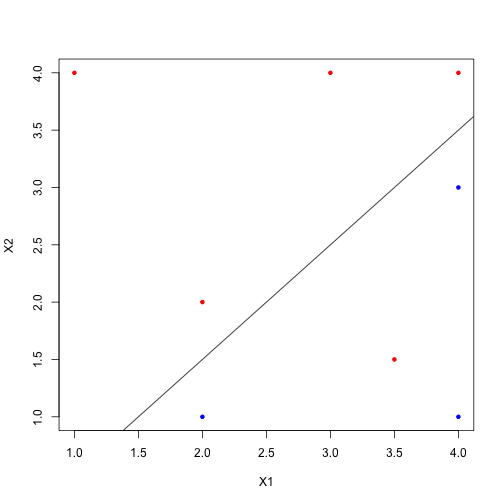
그 어떤 직선으로도 완벽히 data를 분리해 낼 수 없게 됩니다. 하지만 이 또한 머리 좋으신 분들이 방법을 다 생각해 놓으셨으니 걱정하실 것 없습니다 :) 그것에 대해서는 다음 시간에 배워볼게요~