이번에 알아볼 예제는 Python의 Scipy의 optimize 라이브러리 중 fsolve라는 함수를 알아보겠습니다. 이 fsolve를 통해 우리는 $f(x)=0$을 만족시키는 해인 $x$를 찾아낼 수 있습니다. 인자는 2개를 받는데, 첫번째 인자가 $f(x)$이고, 두번째 인자는 초기에 어떤 점에서부터 찾기 시작할 것인지를 나타내는 인자입니다.
자, 그럼 일단 간단하게 $x+3=0$을 만족하는 $x$값을 찾아봅시다. 답이 $x=-3$이라는 것은 쉽게 아시겠죠?
#일단 사용할 라이브러리를 import시킵니다.
>>> from scipy.optimize import fsolve
>>> import numpy as np
#x+3을 리턴해주는 함수를 정의합니다.
>>> line = lambda x: x+3
#fsolve함수를 이용해 초기 x값을 0으로 하여 해를 찾아냅니다.
>>> solution = fsolve(line, 0)
>>> print solution
[-3.]해를 잘 찾음을 확인할 수 있네요.
그런데 $f(x)=0$의 해를 찾아내는 것은, 임의의 두 함수 $g(x), h(x)$가 있을 때에, $g(x)-h(x)=0$ 의 해, 즉 두 함수의 교점을 찾는 것도 가능하다는 의미겠지요!? 먼저, fsolve를 이용하여 교점을 찾아주는 함수를 구현해 보겠습니다.
# 결국 교점을 찾는 것은 f(x)-g(x)=0의 해를 찾는 것입니다.
def findIntersection(fun1, fun2, x0):
return fsolve(lambda x: fun1(x) - fun2(x), x0)그럼 이제 함수 두 개를 만들어서 잘 교점을 찾아내는지 확인해 보겠습니다.
>>> funky = lambda x: np.cos(x/5)*np.sin(x/2)
>>> line = lambda x: 0.01*x - 0.5
>>> result = findIntersection(funky, line, [15, 20, 30, 35, 40, 45])
>>> print "x= ", result
x= [ 13.40773078 18.11366128 31.78330863 37.0799992 39.84837786
43.8258775 ]
>>> print "y= ",line(result)
y= [-0.36592269 -0.31886339 -0.18216691 -0.12920001 -0.10151622 -0.06174122]그럼 찾아진 해가 정확한지 그래프를 그려서 확인해 보겠습니다.
%matplotlib inline
>>> import matplotlib.pyplot as plt
>>> x = np.linspace(0, 45, 10000)
>>> plt.plot(x, line(x))
>>> plt.plot(x, funky(x))
>>> plt.plot(result, line(result), 'o')
>>> plt.legend(['line', 'funky', 'Intersections'], loc=2, bbox_to_anchor=(1.05, 1))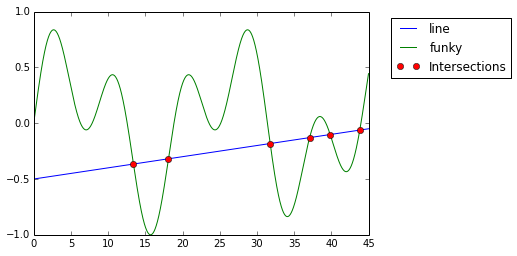
교점을 정확히 잘 찾아내네요. 하지만 여기서 주의하셔야 할 점이 있습니다. fsolve를 할 때에 Newton method를 사용하기 때문에 함수가 convex가 아니면 초기값 x0에 따라서 해를 못찾을수도 있다는 점을 알아두셔야 합니다! 간단하게 예를 들어드리면,
>>> funky = lambda x: np.cos(x/5)*np.sin(x/2)
>>> line = lambda x: 0.01*x - 0.5
>>> result = findIntersection(funky, line, [15, 17, 24])
/System/Library/Frameworks/Python.framework/Versions/2.7/Extras/lib/python/scipy/optimize/minpack.py:236: RuntimeWarning: The iteration is not making good progress, as measured by the
improvement from the last ten iterations.
warnings.warn(msg, RuntimeWarning)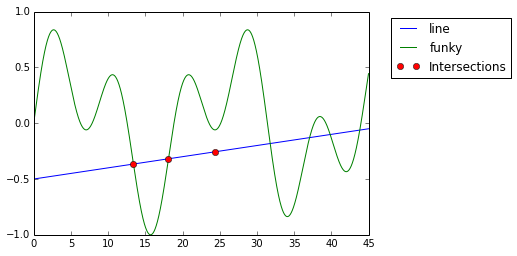
위와 같이 warning과 함께 이상한 해가 아닌 것을 답이라고 내놓았죠? 이렇기 때문에 convex인지 아닌지, 그리고 그에 따라서 초기값을 잘 결정하는 것이 중요한 문제라고 할 수 있겠습니다 :) 어쨌든 그래프를 그려보고 그 점을 정확히 구해내는 것은 할 수 있으니 잘 알아두시면 되겠습니다.