이번에 살펴볼 것은 중요한 자료 구조들 중의 하나인 Binary Heap이라는 구조입니다. 참고 : Wikipedia Heap에는 크게 Min heap과 Max heap이 있는데, 각각 처음 root에 있는 값이 minimum 값이면 min heap, maximum 값이면 max heap이라고 부릅니다. 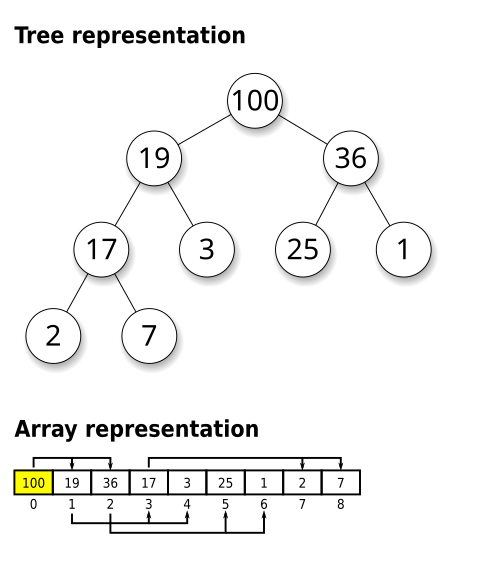
Insert할 때와 Delete할 때가 동일하게 $O(\log n)$ complexity를 가지기 때문에 priority queue를 구현하는데 많이 사용되는 자료구조입니다. 그럼 이제 MinHeap class를 만들어 봅시다.
class MinHeap:
def __init__(self):
self.queue = [None] #0번 index는 비워두겠습니다.파이썬에서 class를 선언할 때에 위와 같이 함수처럼 선언해 줍니다.
그리고 __init__(self)라는 것은 constructor(생성자)로써, 처음 만들어질때 어떤 동작을 하느냐를 결정하는 함수입니다. 여기서는 내부에 list를 생성하고, 0번 index를 편의상 None이라는 값으로 채워 넣겠습니다. **중요한 것 중의 하나는, 클래스 객체 내의 변수를 접근한다거나 하기 위해서는 반드시 self.xxx 이렇게 붙여주셔야 합니다. 그리고 특이한 점 중의 하나는, 클래스 내부의 함수들은 무조건 self를 인자로 받아야 합니다. ** 이는 더 공부가 필요한 부분이니 일단은 넘어가겠습니다.
Heap의 여러 기능 중에 insert 기능을 먼저 구현해 보겠습니다. 알고리즘은 아래와 같습니다.
2. 부모와 비교해 보고 더 작으면 부모와 바꿔주고 그렇지 않으면 멈춘다.
3. Root까지 도착하면 멈춘다.
@staticmethod
def parent(index): #index에 해당하는 원소의 부모 index를 리턴해주는 함수
return index/2
def insert(self, n):
self.queue.append(n)
i = len(self.queue)-1 # Last index
while i>1: # root로 올때까지 부모와 비교하며 더 작으면 바꿔주고 반복한다.
parent = self.parent(i)
if self.queue[i] < self.queue[parent]:
self.swap(i, parent)
i = parent
else: # 만약 부모가 더 작으면 거기서 끝.
break부모가 i/2로 올라가기 때문에 최대 $O(\log n)$번 연산한다는 것을 쉽게 아실 수 있겠죠? 이제 delete 함수를 구현해 봅시다. delete함수의 알고리즘은 아래와 같습니다.
2. 자식들(자식이 하나만 있거나 없을수도 있음)과 비교해서 자신이 더 작으면 거기서 멈춘다.
3. 그렇지 않으면, 자식들(하나면 그냥 바로 바꿔줍니다.) 중에 가장 작은 자식과 바꾸고 내려간 자리에서 다시 2번을 진행한다.
def delete(self):
self.swap(1,len(self.queue)-1) #마지막 원소와 root를 바꿔주고
self.queue.pop(len(self.queue)-1) #마지막 원소를 제거한다.
self.minHeapify(1) #root에서 heapify를 시작한다.
@staticmethod
def leftchild(index): #왼쪽자식 index를 리턴
return index*2
@staticmethod
def rightchild(index): #오른쪽자식 index를 리턴
return index*2 + 1
def minHeapify(self, i): #이 함수가 결국 자식들과 비교해 가면서 내려가는 함수입니다.
left = self.leftchild(i)
right = self.rightchild(i)
smallest = i #일단은 가장 작은 것을 자신으로 놓고
if left <= len(self.queue)-1 and self.queue[left] < self.queue[smallest]: #만약 왼쪽 자식이 존재하고, 가장 작은 것보다 더 작으면
smallest = left #가장작은 것은 왼쪽자식이 된다.
if right <= len(self.queue)-1 and self.queue[right] < self.queue[smallest]: #만약 오른쪽 자식도 존재하고, 그것이 현재까지 최소보다 더 작으면
smallest = right #가장 작은 것은 오른쪽 자식
if smallest != i: #만약 자신이 가장 작은 것이 아니면,
self.swap(i, smallest) #자식들 중 가장 작은 것과 바꿔주고
self.minHeapify(smallest) #recursive call을 하여 내려가서 다시 진행여기서 Heapify라는 함수를 따로 만드는 이유는, 이것이 핵심 알고리즘이고, 다른 곳에도 활용될 수 있기 때문에 decompose 시킨 것입니다.
이제 잘 동작하는지 확인해 봅시다.
>>> import random
>>> minheap = MinHeap()
>>> for _ in range(10):
... minheap.insert(random.randint(1,50)) #랜덤하게 10개의 원소를 입력
>>> print minheap.queue
[None, 3, 7, 16, 18, 28, 38, 25, 44, 41, 45]10개의 원소가 잘 들어가 있는 것을 확인할 수 있네요. 중요한 것은 delete를 해갈 때겠죠?
>>> for _ in range(10): #넣었던 원소들을 하나씩 지우면서 queue를 출력합니다. 결국 작은것부터 지워져나가야겠죠?
... minheap.delete()
... print minheap.queue
[None, 7, 18, 16, 41, 28, 38, 25, 44, 45]
[None, 16, 18, 25, 41, 28, 38, 45, 44]
[None, 18, 28, 25, 41, 44, 38, 45]
[None, 25, 28, 38, 41, 44, 45]
[None, 28, 41, 38, 45, 44]
[None, 38, 41, 44, 45]
[None, 41, 45, 44]
[None, 44, 45]
[None, 45]
[None]None 다음의 숫자들을 보시면 아시겠지만, 작은 순서로 등장함을 확인할 수 있습니다. 잘 구현 되었네요 :) 마지막으로 새로운 생성자를 구현해 보고 마칠게요. 숫자들의 list A가 주어졌을 때, 그것을 heap구조로 만들어 주는 생성자를 만들어 보겠습니다.(아까 class 내부에 선언해 주셔야 합니다!)
def __init__(self, A):
self.queue = [None]+A[:] #list A를 복사해 오는데, 우리의 형태에 맞춰서 복사해 옵니다.
for i in range(len(self.queue)/2, 0, -1):
self.minHeapify(i)여기서 len(self.queue)/2부터 heapify를 실행하는 이유는, 자식이 하나라도 있는 가장 마지막 부모의 index가 여기부터 시작하기 때문입니다. 결국 모든 tree를 부모 자식간에 서열정리를 하게 되는 셈이죠 :) 결과를 확인해 볼까요?
>>> minheap = MinHeap([random.randint(1,50) for _ in range(10)])
>>> print minheap.queue
[None, 2, 6, 17, 34, 40, 30, 45, 41, 40, 50]잘 들어갔음을 확인할 수 있죠? :)