이번에 알아볼 예제는 $a, b, c\ge 0$일때, $a+b+c=n$을 만족하는 $a,b,c$의 조합의 개수를 구하는 것입니다. 가장 컴퓨터스럽게 구하는 방법은, 일일이 숫자를 대입하면서 가능한 조합의 수를 count하는 것입니다. 먼저, $a+b+c=2$의 해를 구한다고 가정해 봅시다. 그러면 이를 그림으로 나타내면, 아래와 같습니다.
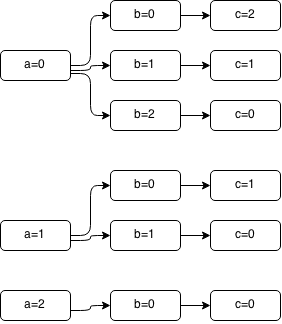
이것은 간단한 경우이지만, 만약에 $n$이 크고, 변수의 수가 많으면 어떻게 될까요? 그러면 이제 문제를 조금 확장해 보겠습니다.
\[a_1+a_2+…+a_k=n\]
저는 이 문제를 구현하기 위해서 먼저 recursive방식을 이용하여 짜 보았습니다. 먼저 $k$개의 변수가 있고, 합이 $n$인 상황을 가정했을 때, $a_1$이 가능한 수는 0에서 $n$까지입니다. 이 때 for문을 이용하여 각각의 값을 대입하고 다음 recursive call로 $k-1$과 $n-a_1$을 부르면서 계속 구해나가는 것입니다. 이 경우, base case는 $k=1$일때, 무조건 1가지만 가능하게 되므로 1을 리턴하면 됩니다. 이를 코드로 작성하면,
def findNumSols_slow(n, k):
if k==0: #혹시 k=0을 넣을 수도 있으니까요^^ 이럴 경우 그냥 0을 리턴한다고 가정합니다.
return 0
if k==1: #변수가 한개만 남았을 경우 1가지만 가능하므로 1을 리턴합니다.
return 1
count = 0 #카운터 변수를 초기화 시키고,
#a_1이 가능한 0에서 n까지 반복하여 값을 대입하면서 recursive call을 합니다.
for i in range(n+1):
count += findNumSols(n-i, k-1)
return count
>>> print findNumSols_slow(5, 3)
21해의 개수를 잘 찾아냄을 확인할 수 있습니다 :) 하지만, 앞서 그림으로 표시했다시피, 이것의 complexity는 상당합니다. 대략적인 upper bound를 잡아보면, \[\begin{aligned} T(n, k)&< T(n,k-1)+n\newline &< T(n,k-2)+n+n\newline &\approx O(n^k)\end{aligned}\] $n,k$가 커짐에 따라서 어마어마한 complexity가 되겠죠?
그럼 이제 dynamic programming의 관점에서 한번 생각해 보겠습니다. 아래와 같은 그림을 그려보시죠.
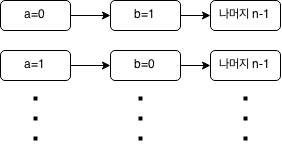
위의 그림과 같이 $a,b$는 다른 값을 가질지라도 셋째 변수부터는 동일한 경우로 취급될 수 있는데, 그때마다 다시 계산을 하면 Fibonacci수를 구할때처럼 엄청난 손실을 보겠죠? 각 $n,k$에 대해서 값을 저장해 놓고 프로그램을 짜게 되면 complexity는 대략 \[O(nk)\] 가 됩니다. 와우.. 엄청난 차이를 가져오겠죠? 그럼 이제 프로그램으로 짜 보겠습니다.
def findNumSols_fast(n, k, cache=dict()):
if k==0:
return 0
if k==1:
return 1
#cache가 이미 해당 tuple에 대한 값을 가지고 있으면 그 값을 리턴합니다.
if (n, k) in cache:
return cache[(n, k)]
count = 0
for i in range(n+1):
count += findNumSols_fast(n-i, k-1, cache)
cache[(n, k)] = count #항상 리턴하기 전에 저장해 주는것을 잊지마세요 :)
return count
>>> print findNumSols_fast(5, 3)
21결과값은 마찬가지로 잘 나오구요, performance를 비교해 보겠습니다.
>>> from time import time
>>> t0 = time()
>>> print findNumSols_slow(70, 6)
17259390
>>> print "걸린시간 : %.2e" % (time()-t0)
걸린시간 : 6.27e+00
>>> t0 = time()
>>> print findNumSols_fast(70, 6)
17259390
>>> print "걸린시간 : %.2e" % (time()-t0)
걸린시간 : 8.91e-03와우.. 거의 1000배 가까이 차이가 나네요… 역시 DP의 힘은 대단한 것 같습니다 :) 근데 여기서 하나 더 언급하고 싶은 것이 있네요. 바로 수학적인 analytic한 solution인데요, 수학이 왜 computer science에서 핵심적인지를 잘 보여주는 예라고 할 수 있겠습니다. 먼저 아래의 그림을 보시죠.
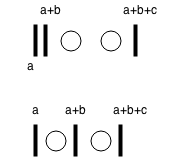
위와 같이 $a+b+c=2$의 해를 구한다고 했을 때, $a+b+c$의 bar는 항상 맨 끝에 위치시켜야 하니 나머지 $n+k-1$의 경우에 대해서 bar를 위치시키는 경우의 수거나 동그라미를 위치시키는 경우의 수가 결국엔 우리가 원하는 solution의 수임을 아실 수 있습니다. 따라서 우리가 구하고자 하는 것은 \[{n+k-1 \choose k-1}={n+k-1 \choose n}\] 이므로, 우리가 이미 구현해 놓은 N choose K의 함수를 가지고 와서 답을 구해보고 성능을 보겠습니다.
def NChooseK(n, k):
numerator = 1
denominator = 1
k = min(n-k, k) #조합의 대칭성을 이용하여 더 적은 수의 연산을 하기 위해서입니다.
for i in range(1, k+1):
denominator *= i
numerator *= n+1-i
return numerator/denominator
>>> t0 = time()
>>> print NChooseK(70+6-1, 6-1)
17259390
>>> print "걸린시간 : %.2e" % (time()-t0)
걸린시간 : 1.91e-04와.. 거의 45배 빠르네요.. 자 이제 확실히 느끼실 수 있겠죠? 우리가 왜 수학을 배워야 하는지요.. :) 수학이 우리를 괴롭히기 위한 것이 아니라 우리를 윤택하게 해주기 위한 수단이랍니다 :) 코딩을 잘 하는것도 좋지만, 수학을 탄탄히 하게 되면 훨씬 더 효율적인 프로그램을 짤 수 있게 됩니다 :) 파이팅!