이번에 살펴볼 알고리즘은 코딩의 꽃, sorting에 관련된 것입니다. 그 중에서도 가장 먼저 생각할 수 있으면서 조금은 비효율적인 bubble sort에 대해서 살펴보겠습니다. (참고: Wikipedia)
Wiki에 아주 좋은 설명 그림이 있네요 ^^
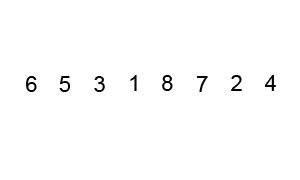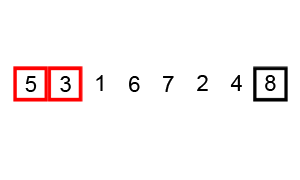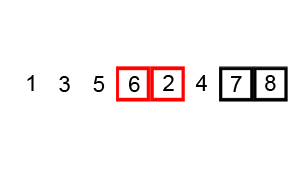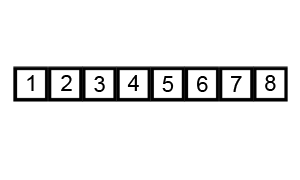
이런 식으로 한번 루프를 돌 때에 두개씩 짝을 지어서 오름차순 내지는 내림차순으로 정렬하는 것입니다. 그러면 결국 Worst case로 처음에 있는 원소가 마지막 원소로 가야하는 경우에, N-1번을 움직여야 하므로 총 \[O((N-1)\times(N-1))\approx O(N^2)\]의 complexity를 갖게 됩니다. 이제 code로 살펴보면,
def bubble_sort(L):
for i in range(len(L)-1):
for j in range(len(L)-1):
if L[j] > L[j+1]:
temp = L[j+1]
L[j+1] = L[j]
L[j] = temp
>>> import random
>>> numList = [random.randint(1,100) for _ in range(10)]
>>> print numList
[81, 92, 17, 90, 66, 55, 15, 56, 84, 86]
>>> bubble_sort(numList)
>>> print numList
[15, 17, 55, 56, 66, 81, 84, 86, 90, 92]오름차순으로 잘 정렬됨을 확인할 수 있죠?? ^^ 그러면 여기서 조금 더 알고리즘을 최적화하는 방법은 무엇이 있을까요?
Worst case에서는 같은 성능을 보일 지는 모르겠지만, 그래도 만약에 이미 많이 정렬이 되어 있는 상태라면 굳이 N-1번의 루프를 반복하는 것보다 정렬이 다 끝나는대로 더 반복하지 않는것이 연산의 효율성을 생각하면 더 좋을 것입니다. 이를 코드로 구현하면,
def optimized_bubble_sort(L):
swapped = True
while swapped:
swapped = False
for i in range(len(L)-1):
if L[i] > L[i+1]:
temp = L[i+1]
L[i+1] = L[i]
L[i] = temp
swapped = True
>>> numList = [random.randint(1,100) for _ in range(10)]
>>> print numList
[92, 56, 40, 90, 38, 57, 94, 8, 36, 38]
>>> optimized_bubble_sort(numList)
>>> print numList
[8, 36, 38, 38, 40, 56, 57, 90, 92, 94]마찬가지로 정렬은 잘 되네요 ^^ 그럼 이제 정말로 효율적인 경우가 있는지 살펴봅시다. 극단적인 예를 들어 이미 정렬되어 있는 list를 정렬한다고 가정합시다. 그러면,
>>> from time import time
>>> sortedList = [range(10000)]
>>> t0 = time()
>>> bubble_sort(sortedList)
>>> print "걸린시간 : %.2e" % (time()-t0)
걸린시간 : 1.16e-04
>>> t0 = time()
>>> optimized_bubble_sort(sortedList)
>>> print "걸린시간 : %.2e" % (time()-t0)
걸린시간 : 8.32e-05시간이 조금은 단축됨을 확인할 수 있죠?? ^^