이번에는 제 포스팅 처음으로 코딩이 없는 포스트를 올리려고 합니다. 그만큼 제게는 충격이었고, 수학자들의 위대함을 새삼 느끼게 되네요! 하버드와 MIT를 방문하니 마구 학구열이 불타네요 :) 어찌됐건 한 예화를 들려드리겠습니다. (참고 : Math Is Fun)
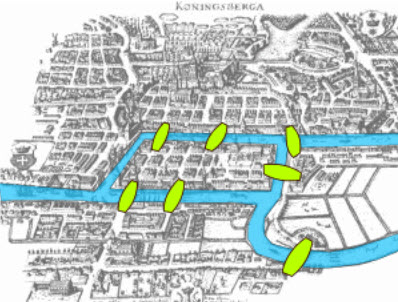
옛날에 Königsberg라는 도시에 Immanuel Kant라는 사람이 살고 있었습니다. 그는 정말 시계처럼 정해진 규칙대로 살아가는 규칙남이었죠. 그러던 어느날 그는 하나의 사실에 충격을 받습니다. "어떻게 내가 집에서 출발해서 각 동네를 찍는데 중복되게 건너지 않은 다리가 없지!?" 결국 그는 이 문제를 그의 친구였던 Leonhard Euler(오일러)에게 부탁하게 됩니다. 오일러는 결코 불가능하다는 것을 증명했고, 수학의 또 하나의 새로운 지평을 여는 역사적인 순간이었죠.
결국 문제는 이것입니다. 도시의 각 부분을 모두 찍으려고 할 때, 다리를 한번씩만 거쳐서 할 수 있을까요?
흔히 말해 이 문제는 우리가 어릴 때 별을 연필을 때지 않고 그릴 수 있는가?의 문제와 같은 문제입니다. 위의 도시는 아래와 같은 그림으로 graph로 표현할 수 있는데요,
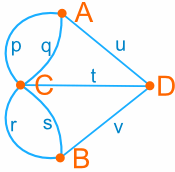
이 graph를 연필을 떼지 않고 그릴 수 있을까요? 이런 모양들은 어떨까요?
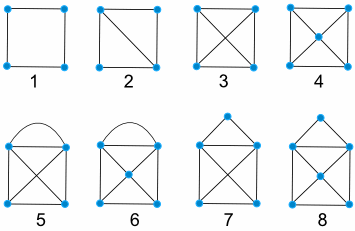
문제를 풀기 전에, Graph의 구조를 살펴보면, graph는 그림에서 보시다시피 Vertex(꼭지점)와 Edge(모서리)의 두 가지로 구성되어 있습니다.
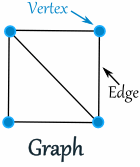
또한, 각 vertex에는 degree라는 attribute이 존재하게 되는데, 몇 개의 모서리를 가지고 있느냐가 바로 degree입니다. Vertex마다 각각 degree를 갖게 되겠죠?
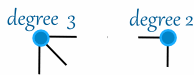
단순히 직접 그려봐야만 알 수 있을 것 같은 이 문제의 답은 수학적인 정확한 해를 가지고 있답니다! 바로 ‘몇 개의 vertex가 홀수개의 degree를 갖는가?’입니다. 결국 연필을 떼지 않고 한번에 그릴 수 있는 경우는,
- 홀수 degree를 갖는 꼭지점의 수가 0개 또는 2개여야 합니다!
- 만약 홀수 degree를 갖는 꼭지점이 2개가 있다면, 그 둘은 반드시 시작점과 끝점입니다.
그럼 어떻게 이런 법칙이 성립할 수 있을까요?? 원리는 간단합니다. 만약 한 번에 그릴 수 있는 graph가 있다면, 한 꼭지점으로 모서리를 그렸을 때, 반드시 다른 꼭지점으로 모서리를 그릴 수 있어야 합니다. 즉, 모서리의 개수가 항상 pair를 이뤄야 한다는 것이죠! 반면, 시작점이나 끝점은 들어오는 모서리나 나가는 모서리가 없기 때문에 그 두 점만 유일하게 홀수인 degree를 가질 수 있는 것입니다.
무릎을 치게 되지 않나요!? 오일러는 이것을 무려 300년 전에 생각해 냈답니다..;; 존경스럽네요.. 이것을 발단으로 Network Analysis라는 분야가 본격적으로 생겨나기 시작했습니다 :)