이번에 살펴볼 예제는 Divide and Conquer라는 알고리즘에 있어서 가장 기본적이면서 핵심적인 스킬을 연습해 볼 수 있는 예제입니다. 앞서 Merge Sort와 Quick Sort에서 이미 다뤘던 개념이고, 하나의 큰 문제를 작은 하위 문제들로 나눠가면서 complexity를 크게 줄이는 방법입니다. 먼저 아래와 같은 주식 가격 정보가 있다고 가정해 봅시다.
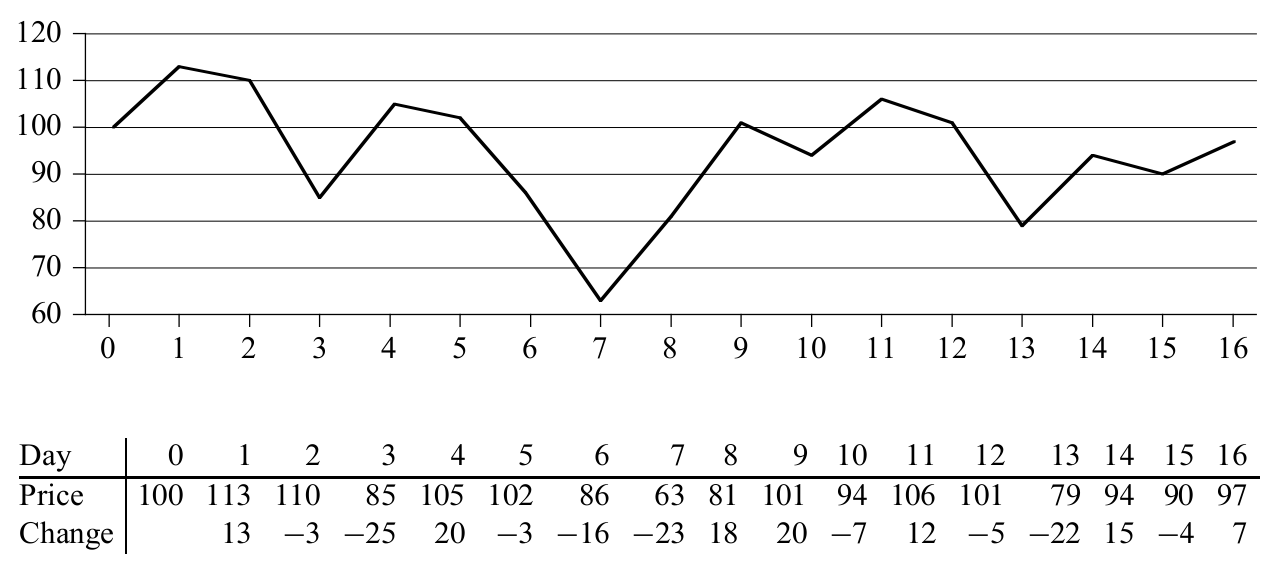딱 한 번 사고 팔 기회가 있다고 가정했을 때, 언제 사서 언제 팔아야 최대의 수익을 낼 수 있을까요?(단, 사는 날짜는 반드시 파는 날짜보다 이전이어야 합니다.)
일단 문제를 다른 관점에서 바라보기 위해서 각 구간의 주식 가격 차이(change)를 구합시다. 위의 그림에서 확인하실 수 있죠? 그럼 최대 수익을 낸다는 것은 어떤 의미일까요? 바로 연속된 일정 구간 내의 합이 최대가 되는 subarray를 찾아내는 문제가 됩니다.
Brute-force solution(무식한 방법?으로 풀었을 때)에 모든 가능한 subarray의 합을 구한 후 최대 합이 나는 지점을 찾으면 됩니다. 이것은 쉽게 떠올리실 수 있겠죠? 그럼 일단 코드로 작성해 봅시다.
def brute_force_findMaximumSubarray(A):
max_sum = -float('Inf')
for i in range(len(A)-1):
for j in range(i, len(A)):
_sum = sum(A[i:j+1])
if _sum > max_sum:
max_sum = _sum
max_left = i
max_right = j
return max_left, max_right, max_sum그럼 이제 우리의 예제에 적용해 보고 올바른 답을 내는지 확인해 봅시다.
>>> price = [100, 113, 110, 85, 105, 102, 86, 63, 81, 101, 94, 106, 101, 79, 94, 90, 97]
>>> change = [price[i+1]-price[i] for i in range(len(price)-1)]
>>> print change
[13, -3, -25, 20, -3, -16, -23, 18, 20, -7, 12, -5, -22, 15, -4, 7]
>>> brute_force_findMaximumSubarray(change)
(7, 10, 43)올바른 정답을 도출하네요 :) 그런데 아시다시피 이렇게 모든 가능한 subarray의 합을 구하는 코드는 $O(n^2)$의 complexity를 갖게 되고 굉장히 느리다고 할 수 있습니다. 어떻게 빠르게 최대 수익 구간을 구할 수 있을까요?
먼저 list A의 low와 high의 사이에 있는 subarray에서 최대 합 subarray를 찾는다고 가정합시다. 중간 지점 mid를 잡았을 때, 최대 합을 갖는 subarray는 다음의 세 가지 구간 중의 하나에 속하게 되어 있습니다.
- 먼저 최대 합 subarray가 완전히
low~mid안에 속할 경우 - 최대 합 subarray가 완전히
mid+1~high안에 속하는 경우 - 마지막으로 최대 합 subarray가
mid를 끼고 애매하게 걸쳐있는 경우
아래 그림을 보시면 더 이해가 잘 되실 것입니다.
이렇게 되면 세가지 경우 각각의 최대 합 subarray들을 비교해서 그 중에 가장 최대의 합을 갖는 subarray를 찾아서 리턴하면 되겠습니다. 이 때 complexity는, \[\begin{aligned} T(n)&=2T(n/2)+n\newline &=O(n\log n) \end{aligned}\] 가 되어 앞서 구한 $O(n^2)$를 압도하겠죠? :)
그럼 먼저 mid를 걸친 최대 합 subarray를 찾는 함수를 정의해 봅시다.
def findMaxCrossingSubarray(A, low, mid, high):
left_sum = -float('Inf')
_sum = 0 #built-in 함수 이름과 동일하지 않게 이름을 붙여줍시다.
## 일단 mid를 기준으로 왼쪽으로 search해 나가면서 최대합을 찾고 왼쪽 index를 찾습니다.
for i in range(mid, low-1, -1):
_sum += A[i]
if _sum > left_sum:
left_sum = _sum
max_left = i
right_sum = -float('Inf')
_sum = 0
## 마찬가지로 이번에는 mid+1부터 오른쪽으로 search해 나가면서 최대합을 찾고 오른쪽 index를 찾습니다.
for j in range(mid+1, high+1):
_sum += A[j]
if _sum > right_sum:
right_sum = _sum
max_right = j
# 결국 mid를 지나는 최대 합 subarray를 찾을 수 있습니다.
return max_left, max_right, left_sum+right_sum이제 전체적으로 최대 합 subarray를 찾는 Recursive 함수를 만들어 보겠습니다.
def findMaximumSubarray(A, low, high):
if high == low: #base case - 한 개의 원소만 있을 경우
return low, high, A[low]
else:
mid = (low+high)/2 #일단 mid를 low와 high의 중간으로 설정한 후,
#왼쪽 절반에서 최대 합 subarray를 찾아 리턴받고,
left_low, left_high, left_sum = findMaximumSubarray(A, low, mid)
#오른쪽 절반에서 최대 합 subarray를 찾아 리턴받고,
right_low, right_high, right_sum = findMaximumSubarray(A, mid+1, high)
#마지막으로 mid를 포함하여 가로지르는 최대 합 subarray를 리턴 받고
cross_low, cross_high, cross_sum = findMaxCrossingSubarray(A, low, mid, high)
## 셋의 크기 비교 후 최대 합을 갖는 것으로 리턴합니다.
if left_sum >= right_sum and left_sum >= cross_sum:
return left_low, left_high, left_sum
elif right_sum >= left_sum and right_sum >= cross_sum:
return right_low, right_high, right_sum
else:
return cross_low, cross_high, cross_sum일단 기본적으로 잘 동작하는지 살펴봅시다.
>>> findMaximumSubarray(change, 0, len(change)-1)
(7, 10, 43)동일한 결과를 가져오네요. 그럼 끝으로 성능이 대체 얼마나 좋아지길래 이 난리인지 살펴봅시다.
>>> import random
>>> from time import time
#임의로 0~200사이의 정수 1000개를 주식 가격으로 발생시킵니다.
>>> price = [random.randint(0, 200) for _ in range(1000)]
>>> change = [price[i+1]-price[i] for i in range(len(price)-1)]
>>> t0=time()
>>> print brute_force_findMaximumSubarray(change)
(392, 446, 200)
>>> print "걸린시간 : %.2e" % (time()-t0)
걸린시간 : 1.81e+00
>>> t0=time()
>>> print findMaximumSubarray(change, 0, len(change)-1)
(392, 446, 200)
>>> print "걸린시간 : %.2e" % (time()-t0)
걸린시간 : 7.17e-03무려 250배 차이가 나네요! 고작 1000개 수밖에 안했는데, 만약 $n$이 커지면 이 차이는 더 심해지겠죠? Divide and Conquer의 힘을 다시 한 번 느낄 수 있었습니다!